时间序列数据的聚类有什么好方法？

数据挖掘顶会SIGKDD 2017年的文章《Toeplitz Inverse Covariance-Based Clustering of Multivariate Time Series Data》介绍了一种聚类多元时间序列的方法。该文荣获 KDD 2017年Research Track的Best Paper亚军。该文的论文，介绍视频，代码以及PPT地址链接依次如下所示：

（注：上述最后一个链接，即该文对应的PPT收录于Slideshare上，Slideshare下载需要付费，如果想要免费下载，可以选择如下的Slideshare downloader）

另外，文中所提到有关交替方向乘子法(alternating direction method of multipliers，ADMM)的公式推导部分可参考该文作者，也是Stanford的统计学大牛Stephen Boyd有关ADMM的论文《Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers》（主要参考该文的6.5章节：即稀疏协方差的选择（Sparse Inverse Covariance Selection）一章）。该文链接如下：

1. 摘要部分：本文主要研究多元时间序列的时序聚类问题，即同时对多元时间序列进行分割和聚类（聚类须考虑时间戳的连续性，即尽量保证相邻的时间戳被聚在同一类中）。除此之外，如何生成可解释性较强的聚类结果同样是一个极具挑战性的问题。因此，本文提出了一种新的基于模型的聚类方法，称之为Toeplitz逆协方差聚类（Toeplitz Inverse Covariance-based Clustering，TICC）。TICC方法可以较好的实现对多元时间序列进行时序聚类，并且该方法将每个聚类定义为依赖网络（correlation network）或马尔可夫随机场(Markov random field，MRF)，以表征该聚类中不同观测值之间的相互依赖性，从而极大的提升了算法本身的可解释性。在问题求解方面，文章使用期望最大化算法（EM）的变体，分别通过动态规划（dynamic programming）和交替方向乘子法(alternating direction method of multipliers，ADMM)推导出封闭形式的可扩展解决方案。文章通过在一系列综合实验中将TICC与几个最先进的基线（baseline）进行比较来验证TICC方法，然后在汽车传感器数据集上演示如何使用TICC在现实世界场景中学习可解释的集群。

2. Introduction以及问题定义(problem setup)部分：

本文所研究的多元时间序列时序聚类问题比标准时间序列分割更困难，因为该问题不仅需要实现分割功能，并且需要对重复出现的模式进行识别；这一问题同样也比子序列聚类更难，因为该问题需要尽可能的将相邻时间戳聚为一类。此外，即使能够同时对多元时间序列进行分割和聚类，对聚类结果生成一个可解释性较强的表述又是一个极具挑战性的问题。为解决上述问题，本文对多元时间序列的时序聚类问题进行了如下定义：

考虑如下原始(original)多元时间序列：

我们的目标是将上述 个观测值聚为 个类。往常有许多时序聚类的工作，这些工作操作的数据最小粒度为单个时间戳（如上文中的 ），通过施加正则化等约束尽量使得相邻单个时间戳被聚为一类，即可解决时序聚类问题。本文与寻常的时序聚类工作有所不同，本文用于聚类的最小数据粒度不是单一的时间戳 ，而是在时间序列中将每个时间戳放置在其前述背景下进行考虑（譬如在汽车驾驶的研究背景下，一次观察可能会显示汽车的当前驾驶状态，但一个短暂的窗口，即使只持续几分之一秒，也可以让我们更为全面的了解汽车的行驶状态）。因此，本文定义一个时间窗口，大小为 ，并将 之前相邻的 个时间戳拼接成一个向量 作为聚类算法的最小数据粒度，这样整个聚类输入的数据矩阵为：

在定义完TICC处理的数据最小粒度 以及整个输入的数据矩阵 后，接下来将对本文最为核心的假设进行说明：本文希望通过TICC聚类得到的每一个簇都代表原始多元时间序列中一种特定的“状态”，当原始多元时间序列处于这种特定的状态时会保留一定的时不变结构，该结构会在整个簇所涵盖的时间窗范围内持续存在，而与时间窗的起点无关。为了将上述核心假设，尤其是假设中的时不变结构显式化，文章引入了Toeplitz矩阵结构，用于构造能够描述各sensor之间相关性的逆协方差 。我们首先了解一下Toeplitz矩阵结构是什么样的：

当然，上述是一般Toeplitz矩阵的定义，其中 和 的值不一定相等，即上述Toeplitz矩阵不一定是对称阵。更为特殊的对称Toeplitz矩阵如下图所示：

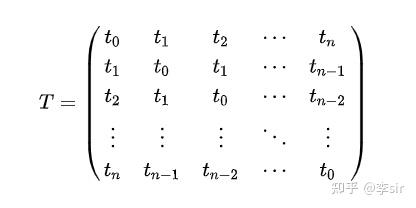
本文中所定义的能够描述各sensor之间相关性的逆协方差 即为对称Toeplitz矩阵，其公式如下：

在上式中， , ( 即 矩阵中 行 列的元素)代表当前时刻sensor i与sensor j的依赖关系，依次类推， 代表当前时刻sensor i与后一时刻sensor j之间的依赖关系， 代表当前时刻sensor i与后二时刻sensor j之间的依赖关系。总的来说，文章将簇的表征 构造为Toeplitz矩阵，则可以保证：只要属于该簇，则固定顺序时间戳所包含的所有sensor的依赖关系都保持不变。下面结合该文章的封面图，详细的解释一下引入对称Toeplitz矩阵结构的 所描述的时不变结构究竟是什么样的。

以图3中cluster A的三层依赖网络结构为例（由于图中绘制成三层网络结构，因此我们可认为 ），首先：蓝色，紫色以及橙色三层，每层之间的图都相同，这对应了上述 矩阵中主对角线元素都相同，为 的事实；同时，蓝色与紫色层间边的位置和紫色与橙色层间边的位置相同，这对应了上述 矩阵中一行二列以及二行三列元素相同，为 的事实。换句话说，任选cluster A中的任意一时间戳，其对应的所有sensor与前置时间戳所对应的所有sensor，包括与后置时间戳所对应的所有sensor之间的依赖关系都是保持不变的，和cluster A何时开始以及合适结束没有任何关系，此种性质文中称之为时不变性。

文章的最终目标是求解 个高斯逆协方差 及其分配集 ，其中 。因此，多元时间序列的时序聚类问题的整体目标函数定义如下：

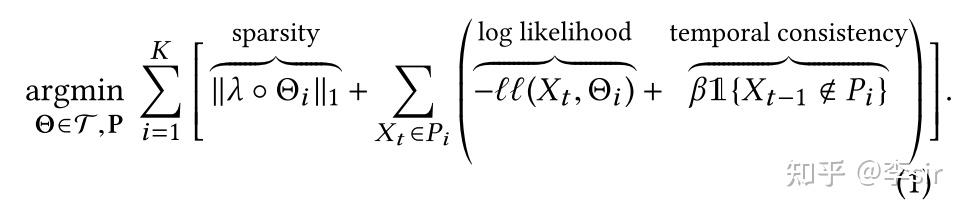
在上式中，我们要尽可能的保证每个 是稀疏的（即每个 拥有尽可能多的0，仅有少部分元素不是0，这样可以增加可解释性），因此需要使第一项 ，即 的L1范数取最小值（其中为参数），同时，为了确保使相邻时间向量 以及 尽可能的聚为一类，我们需要使目标函数中的最后一项，即 取最小值（ 为参数）。最后，我们需要采用最大似然估计，因此我们需要保证目标函数最中间的一项，即 取最小值，其中 定义如下：

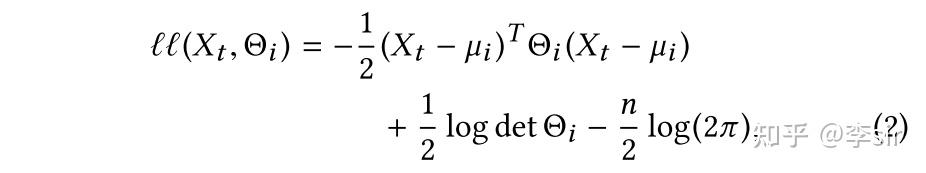
综上所述，整个TICC问题中总共涉及到4个超参数，包括正则化参数 以及 ,时间窗大小 以及聚类数 。尽管TICC问题中存在的超参数较多，但该文章在后续实验部分对所有参数单独进行了灵敏度实验，实验结果表明：该文提出的算法鲁棒性较好，算法对于参数在相当大范围内的改变都可以取得良好的效果。

3. 问题求解部分：

目标函数（1）式是一个混合的组合和连续优化问题。在目标函数中总共有两组变量需要求解，即：集群分配（cluster assignment） 和逆协方差 ，两者耦合在一起以使问题高度非凸。针对上述问题，文章采用期望最大化算法（EM算法）的变体进行求解，即在将更新点分配参数 以及更新簇参数 之间交替进行最小化。

首先，我们初始化各个簇参数 （各个逆协方差） ，并且固定这些参数，以更新点分配参数 。由于 固定，因此 结果与最小化无关，故从目标函数中删去，因此，现阶段子问题转化为如下目标函数：

问题（3）可通过动态规划求解，求解过程类似隐马尔可夫模型中的维特比路径问题，感兴趣的读者可以参考这篇文章：

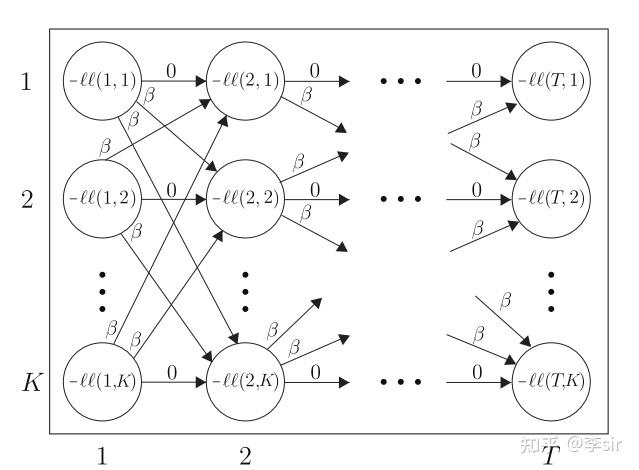
在更新完点分配参数 之后，我们固定 ，以交替更新逆协方差 。这样，由于 已经被固定，因此总目标函数中的 将变成不影响最小化目标函数的常数 ，这样，该阶段的子问题目标函数将定义如下：

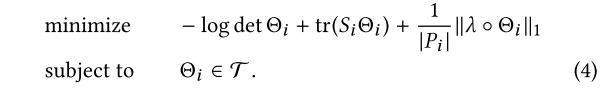
文章采用交替方向乘子法(alternating direction method of multipliers，ADMM)去求解上述问题。对推导该部分公式感兴趣的读者请参考Stephen Boyd有关ADMM的论文《Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers》（主要参考该文的6.5章节：即稀疏协方差的选择（Sparse Inverse Covariance Selection）一章），里面有较为详细的公式推导步骤，且与本文中的公式推导一一对应。

4. 实验部分：详情请参考原论文。