量子纠缠被证实意味着什么?
世界的本质,居然真是量子化的。
而上帝,真的是在掷骰子......
「量子纠缠」这个名词可以说是近年来,在量子物理领域里,除了量子计算机以外,被普通大众媒体提及最多的网红破圈词汇了。
当然,还有很多和量子纠缠相关的名词,也经常被媒体提及。
比如量子加密通讯,密集编码,量子隐态传输等等。
这些名词经常被提及,其中一个重要的原因就是:这是在各种玄妙的量子技术领域中,最前沿最接近实用化的技术之一。
同时,我们国家在这项技术上,又还处于非常领先的地位。
所以媒体们,也很爱提到我们在这方面取得的科技成就和荣誉,顺便也给大家普及了这些高冷无比的科学名词。

那么所谓量子纠缠究竟是什么呢?
是不是像某些媒体描述的那样,可以帮助人们实现绝对安全的远程通讯,构筑无法干扰、无法窃听的保密通信网,或者是实现无视距离的超光速信息传递呢?
此外,这个现象是不是也可以和之前的量子现象一样,我们也同样可以用虚拟世界的视角来帮助认识和理解呢?
大家不要着急,我们还是先了解一些基础知识。
我们先看看量子纠缠到底是什么意思。
所谓量子纠缠,其实就是指微观世界里面,发生的一种特殊的多粒子的耦合现象。
通俗来说,就是几个粒子联成了一个整体系统了。
不过它们联成的不是一个整体,而是一个整体系统,也就是说每个粒子还是单独存在的,而且可以分开。
但是从关系上呢,它们之间又存在某种不可分割的整体关联。
一旦粒子之间有了这种纠缠关系之后,这些彼此纠缠的粒子不管身在何方,它们之间都能瞬间互相影响。
而且这种影响,不随距离的改变而消失。
彼此之间的影响,似乎也没有任何速度上的限制。

比如说,一对相互形成纠缠的粒子。(我们把它们比作一对兄弟吧)
我们把这对兄弟粒子彼此分开,然后让它们向相反方向飞去,并让它们尽可能地飞得相距更远一些,比如让它们相距百万甚至千万公里以上。
然后,这时候我们观测其中一个「哥哥粒子」的某些属性,比如观测它的自旋方向。
一旦当我们观测到这个「哥哥粒子」自旋方向后,另一个「弟弟粒子」就能同时就能感应到,它的兄弟被观测了。
于是,它马上也就显示出一个跟它「哥哥」完全相反的自旋方向来,以保持他们彼此绝对互补。
你瞅瞅这个过程,是不是会感觉,其实并没有那么复杂难懂。
也许这对粒子在分开时候自旋方向本来就是相反的,它们只不过保持了角动量守恒。
所以不管跑多远,你看了其中一只,自然就知道另一只的方向了。
就像两只鞋子,本来就是一对。
不管你把它们分开多远,你只要看到一只是左脚的,自然马上知道另一只就是右脚的嘛。
这难道有什么奇怪的地方吗?
问题自然没有那么简单,科学家们自然也不会连这种基本关系也会好奇。
科学家们深入研究了这个问题后发现,纠缠粒子之间的关系,并没有角动量守恒这么单纯。
它们之间,具有着更深入的互补特性。
这就值得好奇一下了。
其实最先发现这个问题的,正是大名鼎鼎的爱因斯坦。
爱因斯坦,正是在和玻尔的哥本哈根学派,论战的过程中,把这个问题先提出来的。
提到爱因斯坦和玻尔的世纪大论战,话又要说回我们之前提到的物理史上那个最激动人心的年代:新量子力学诞生的年代。
当时,爱因斯坦作为旧量子理论的拥护者和以玻尔为代表的新量子理论开创派——哥本哈根学派之间发生了激烈的争执。
爱因斯坦,曾经尝试用一个「光箱思想实验」挑战玻尔的量子理论。
可惜并未成功。
反而,还被玻尔利用爱因斯坦自己的相对论,进行了成功的反驳,击退了爱因斯坦的第一次挑战。
但是,爱因斯坦肯定不是会轻易认输的角色。
几年后,爱因斯坦卷土重来,再次向哥本哈根发起了新的挑战。
这次爱因斯坦利用的武器就是与量子纠缠相关的一个新的思想实验:EPR 佯谬问题。
什么是 EPR 佯谬问题呢?
EPR 佯谬,就是针对量子纠缠现象中,两个粒子的相关性提出的。
在当时,量子的「不确定性」和观测导致「坍缩」的特性已经都被大家所认识了。
两个粒子发生纠缠的时候,也会有这样的现象存在。
只不过呢,两个纠缠的粒子被观测的时候,会同时坍缩。
坍缩后两个粒子,就会保持完全相反的互补状态。
这个现象其实是已经都被大家所了解的。
但爱因斯坦提出:
假如两个粒子发生纠缠之后,设法将这两个粒子分开得足够远,远到之间的距离,连光传播也要很久的时间,比如一百光年那么远。
此时我们观测其中某个粒子,按照量子理论,另一个粒子的状态,就会瞬间确定。
而两个粒子,在属性上,又需要保持「完全互补」的关系。
那么这种关系的确定过程,如果是瞬时的,岂不是就超越了光速吗?
那么要解释这种现象,只有两种可能:
第一种可能,是有某种机制,让信息超越光速,进行了传播,瞬间协调了它们之间的属性;
第二种可能,则是这两个粒子,事先约定好了某种互补状态,然后一直保持着状态互补关系。
这两种可能解释,其实就意味着对整个世界的两种解释方式:
前者,如果我们相信,是由某种超光速机制在协调两个遥远的粒子。
那么这个世界,似乎在微观层面就有一些和宏观层面不一致的神秘机制在起作用。
而如果是后者,那么就只是一个简单问题了,只是我们的认识不足,还有一些物理学的隐藏参数没有发现而已。
粒子之间的瞬间协同性,其实只是一种「假象」,是我们现阶段知识不足造成的而已。
伟大如爱因斯坦,怎么可能认同前面那种,如同神棍的逻辑呢?
他当然认为应该是后者,两个粒子之间一定存在某种「隐变量」在制约它们的行为而已,哪里有什么神秘机制。
更何况,当年也没有电子游戏,这样的虚拟体验可以启发思想,不是吗?
于是,爱因斯坦就拿出了这个 EPR 佯谬问题,很严肃地告诉玻尔。
你们除非证明两个纠缠粒子之间的关系是前者,而不是后者。
否则,你们整个量子力学体系就是错的。
世界不是你们想象出来的,它还是经典的、定域的、实在的!
好,现在球踢给哥本哈根学派了,玻尔他们现在要怎样应对爱因斯坦的挑战呢?
玻尔面对挑战自然不会轻易认输。
他作为新时代量子理论的奠基者之一,怎么可能向爱因斯坦的旧理论屈服呢?
就算是他还没玩到电子游戏,玻尔也能感觉出,这个世界背后,一定有某种深层机制突破了定域和实在性。
他果断应战,准备设计实验来证明爱因斯坦错了。
玻尔要如何证明爱因斯坦是错的呢?
玻尔首先要证明,两个粒子之间的协调性速度是远比光速快的。
这比较好办。
我们设计实验,可以把两个粒子分别引到足够远的距离。
然后用超过它们可能利用光速彼此联系的时间,来比对它们的状态就好了。
(比如现实中可以用长光纤,把纠缠的光子对,分别分离、引导开来实现)。
其次,玻尔还要证明,两个粒子之间的协调性是瞬时同步产生的,而不是它们事先约定好的。
我们要证明两个粒子之间,没有任何事先的神秘约定,那这要如何证明呢?
俗话说,瞌睡碰到枕头,真是巧了。
这边正好有一个爱因斯坦的「大粉丝」,听到了这个事情。
他就是北爱尔兰的物理学家,约翰·斯图尔特·贝尔(John Stewart Bell)。
贝尔了解了双方争论之后,当然认为爱因斯坦是对的。
这个世界,怎么可能会出现违反直觉和常识的事情呢?
于是为了帮助爱因斯坦,贝尔反复琢磨了双方的观点。
在 1964 年的时候,他突然想到了一个数学方法,可以把两者的观点,给明确地表述出来。
贝尔用了一个不等式,来表示出了两者,在协调性上的数学区别。
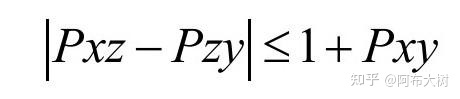
贝尔认为,只要这个不等式成立,那么爱因斯坦就是对的。
两个粒子之间,就一定有事先约定好的方案。
如果不成立,那么玻尔就是对的。
两个粒子之间,没有什么事先约定的方案。
当然,他认为很显然这个不等式应该成立嘛。
不然他为什么不把符号倒过来,用成立来对应玻尔的理论呢?
不过,不管怎样,科学家一致认为这个不等式是对爱因斯坦和玻尔两人争论,或者说是对世界到底是经典的,还是量子的,最为明确的一个数学总结。
而且,这个不等式还比较好验证。
不过我们作为普通读者,怎么才能理解这个公式到底说的是什么呢?
我们也能用虚拟游戏的视角,来理解贝尔不等式的含义吗?
当然可以。
我们现在就尝试用游戏视角,来解释一下这个物理学上最重要的公式之一。
话说在虚拟世界的量子游戏里,我们用系统生成了一对宝箱,系统生成的每对宝箱里面都有一只漂亮的蝴蝶精灵。

我们已知,宝箱里面的蝴蝶精灵的颜色只有白色和黑色。
而每对宝箱里的蝴蝶颜色,则一定是相反的,它们是一对「双子」精灵。
那么毫无疑问,如果有一对宝箱,那么无论什么时候,我们打开其中一只宝箱,看到了里面的蝴蝶的颜色的话,就能马上知道另一只宝箱的蝴蝶颜色。
但是这个游戏的设计师告诉我们,这种成对宝箱的程序实现方式,其实有些区别的。
具体说就是成对宝箱其实有两种实现方式:
一种是,事先就生成好一对双子蝴蝶,然后再分别装在不同宝箱里。
这种,先有蝴蝶,再装进宝箱的方式,我们命名为「传统宝箱」;
而另一种呢,则是在你打开成对宝箱中的任意一只的一瞬间,才马上执行生成蝴蝶的代码。
在两只箱子里,立刻生成一对颜色相反的双子蝴蝶。
我们将这种宝箱命名为「量子宝箱」。
于是游戏的设计师想挑战我们,想让我们试试看,能不能通过观察分辨出哪一对宝箱是传统宝箱,哪一对是量子宝箱。
这个挑战看起来似乎不可能完成。
因为简单从开箱后的观察结果来看,似乎两种形式的宝箱都是完全一样的。
两种都是装着颜色相反的双子蝴蝶而已,我们似乎无法分辨两者有什么不同。
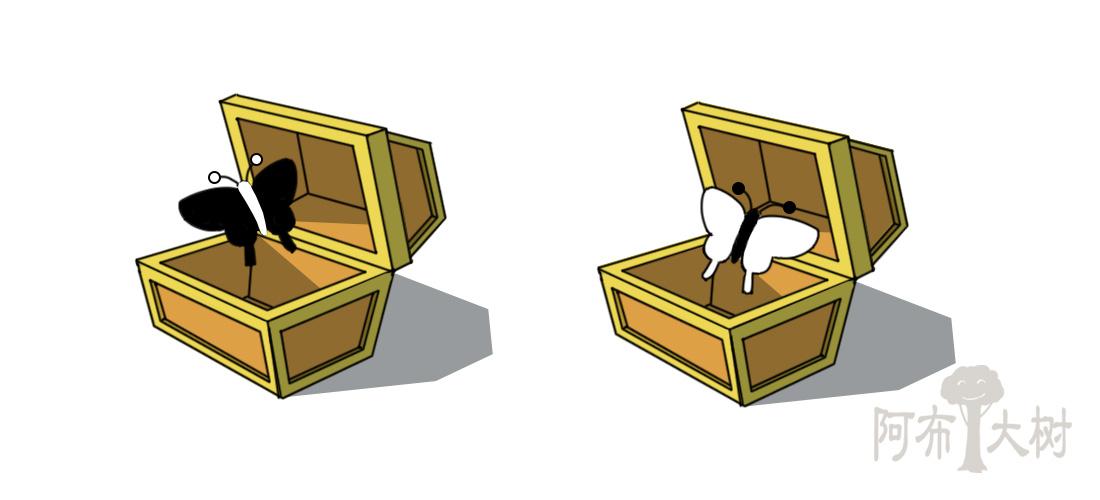
但是,我们玩家都是很有耐心的,经过认真的反复摆弄两种不同的宝箱,重复开箱过无数次以后,我们还是发现了一些差别。
我们发现,每个宝箱里面的蝴蝶颜色其实是由三个部分构成的。
分别是「触角」、「翅膀」和「身体」。
每个部位都有可能是「黑色」和「白色」两种颜色中的一种。
不过每次开箱的时候,蝴蝶身上的颜色都是随机产生的。
当我们打开 A 宝箱的时候,我们如果看到蝴蝶精灵是「黑触角」+「白翅膀」+「黑身体」。
那么我们打开另外一个 B 宝箱,看到的蝴蝶精灵就必然是「白触角」+「黑翅膀」+「白身体」。
完全相反。
如果 A 宝箱看到的是「白触角」+「黑翅膀」+「黑身体」。
那么 B 宝箱里的蝴蝶就一定是「黑触角」+「白翅膀」+「白身体」。
一点都不会错。
那么,两只宝箱里蝴蝶的各部位颜色对应得很好,我们怎么才能分辨出差别呢?
我们仔细思考了一下,传统宝箱和量子宝箱之间的逻辑。
突然我们意识到,它们之间的差别就在于,是否提前约定好了。
传统宝箱里面的蝴蝶精灵,是事先生成好的。
那么两个蝴蝶之间,肯定已经约定好了一套对应的方案,它们才可能做到完全互补。
那么蝴蝶们需要约定好几套方案呢?
因为蝴蝶身上有三个部位可以变化颜色,那么我们排列组合一下就知道,总共需要八套方案。
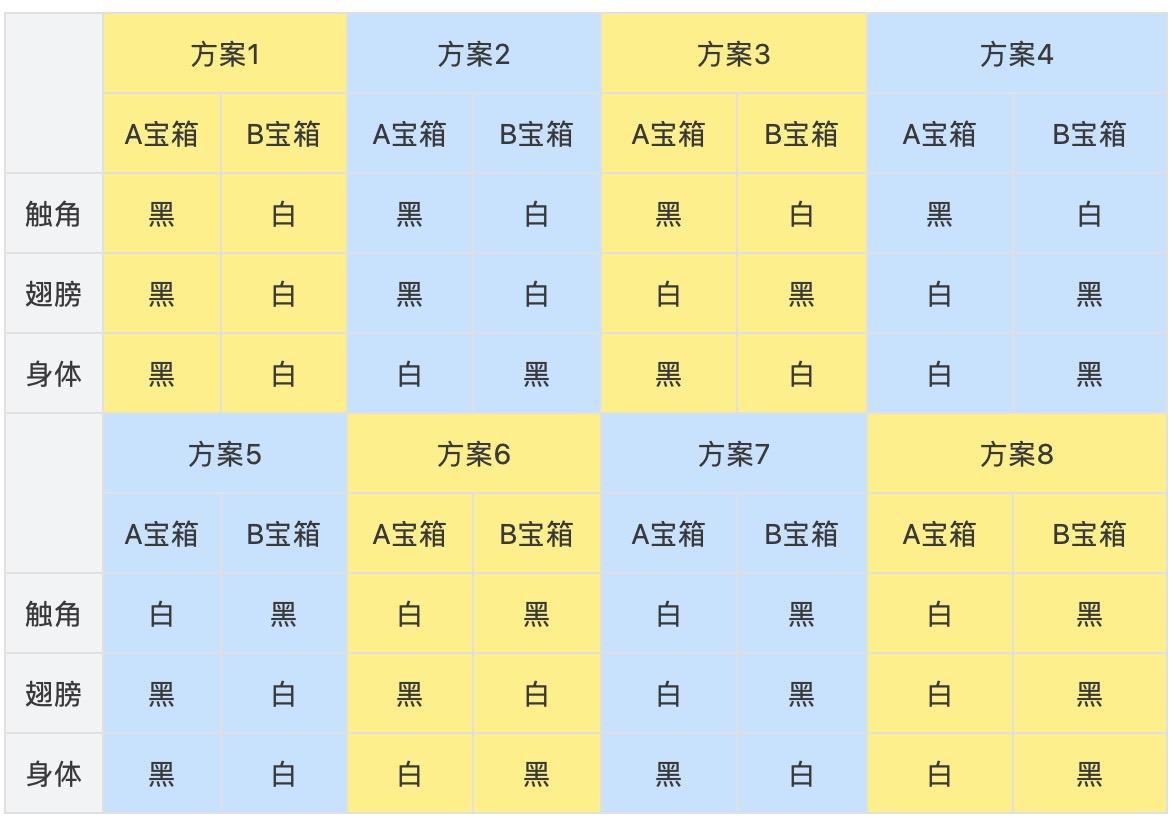
也就是说,如果是传统宝箱的生成方式的话,那么两只蝴蝶精灵,必须先定好用这八套方案中的某一套,来生成各部位的颜色。
一旦定好就不能更改了。
而量子宝箱不同。
量子宝箱里面的蝴蝶,是先不定好颜色方案的,等着开箱的时候,再随机同步生成。
换句话说就是,量子宝箱里面的蝴蝶,处于一种什么情况都可能存在的叠加态中。
在打开宝箱之前,它是没有具体颜色的。
必须等到观测的时候,才会给出它的具体颜色。
那么就算这样,两者有什么区别呢?
我们来另辟蹊径一下。
 新公网安备 65010402001845号
新公网安备 65010402001845号