台风「贝碧嘉」登陆，上海中心大厦千吨阻尼器开始摆动，阻尼器起到哪些作用？工作原理是什么？

发布时间：

2024-09-23 21:48

阅读量：

引言

我国沿海地区常年受台风侵袭，尤其是东南部地区。当强风来袭，强大的风力能让树木折断，广告牌乱飞，甚至摩天大楼也必不可免会产生摇晃。

图 1: 台风中的摩天大楼

我们知道，重心越高的物体也就越容易倒，但上海中心大厦、广州塔等摩天大楼为何能在台风中屹立不动，安然无恙呢？这实际上要归功于摩天大楼的外形的设计和内置的阻尼器。

图 2: 风作用在大楼单位面积上的力

首先我们先了解一下为什么微风都能撼动摩天大楼？实际上，地面上感觉到的微风到了 300 米的高度，风速能达到数十米每秒。风的作用可使摩天大楼每平方米承受 8 公斤的力（图 2），摆动幅度达一米！这种振幅下，即使建筑物的结构仍然完好，也会导致楼内人员严重不适。

图 3: 风吹过迪拜塔后形成的卡门涡街

更严重的是，风绕过摩天大楼时，会在大楼后方形成不对称的漩涡（图 3）[1]，称为卡门涡街。漩涡从大楼两侧交替脱落时，会作用于大楼一个交变的周期激励，引起大楼的周期性振动。当流体流速达到某一程度，激励频率与大楼固有频率一致时，将引发共振。此种情况下，大楼的晃动幅度会越来越大，甚至倒塌。赛格大厦的剧烈摇晃很可能就是卡门涡街造成的。因此，侧向挠度（摇摆或漂移）、振动和建筑物加速度是结构工程师在高层结构设计中需要仔细考量的重要标准。

图 4: 上海中心大厦

减少摩天大楼的摇摆和振动的方法有很多[2]。首先，可以在设计大楼外形时纳入空气动力学的考虑。例如上海中心大厦利用不对称形体、锥形建筑轮廓和圆角设计使建筑风荷载减少了近 1/4（图 4）；韩国首尔的乐天世界大厦，顶部楼层使用了一种斜交网络桁架结构来分散风力作用（图 5）。

图 5: 首尔乐天大厦

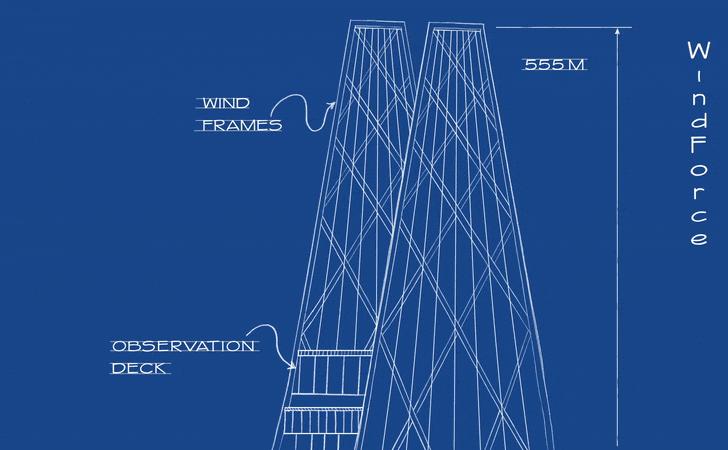
即使如此，如果受到强风的影响，高层建筑还是会不可避免地会晃动（图 6）。

图 6: 强风下摩天大楼的振动（无风阻尼器）

因此，上海中心大厦、广州塔等许多高层建筑还额外安装了称为“调谐质量阻尼器（Tuned mass damper, TMD）”的配重（图 7），俗称风阻尼器（下文简称为“阻尼器”）。

图 7: 强风下摩天大楼的振动（有风阻尼器

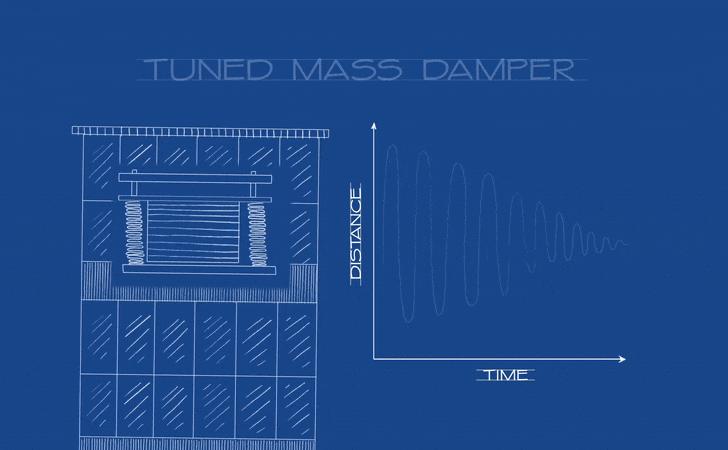
其中最为有名的是台北 101 大厦（图 8），其顶端悬挂一个重达 660 多吨的金属球形阻尼器（图 9）。

图 8: 台北 101 夜景

图 9: 台北 101 的风阻尼器

当建筑物在风的作用下晃动时，风阻尼器会像钟摆一样运动，以吸收建筑物的动能。并由摆球与建筑物之间的液压缸将动能转化为热量释放（图 10），因此建筑物的稳定性得以保持。

图 10: 风阻尼器的工作原理

综上所述，安装风阻尼器是高层建筑提高防风抗震能力的有效手段。本文将通过实验演示和数学模型，定性和定量地分析风阻尼器在高层建筑防风抗振动中的作用，并通过数学模型确定出高层建筑防风抗振的最佳风阻尼器配置。

实验

针对风阻尼器的抗振效果，已经有不少人做过演示实验[3-5]。根据振动方式，风阻尼器主要可以分为平移和摆式阻尼器，例如台北 101 的风阻尼器就属于摆式阻尼器。两种阻尼器的演示实验分别如图 11 和 12 所示。两实验中都可以明显看出，阻尼器可以有效降低主结构的晃动。

图 11: 平移调谐质量阻尼器实验

平移阻尼器实验装置（图 11）主要由能够自由晃动的白色框架（主结构）和包含阻尼弹簧的黄色滑块（阻尼器）组成。

图 12: 摆式调谐质量阻尼器实验

摆式阻尼器实验装置（图 12）主要由能自由晃动的金属塔楼（主结构）和浸入粘性液体的钨制球形摆（阻尼器）组成。实验中，稍微推一下主结构，使其离开平衡位置，观察有无阻尼器情况下主结构的振动。

图 13: 平移调谐质量阻尼器实验结果

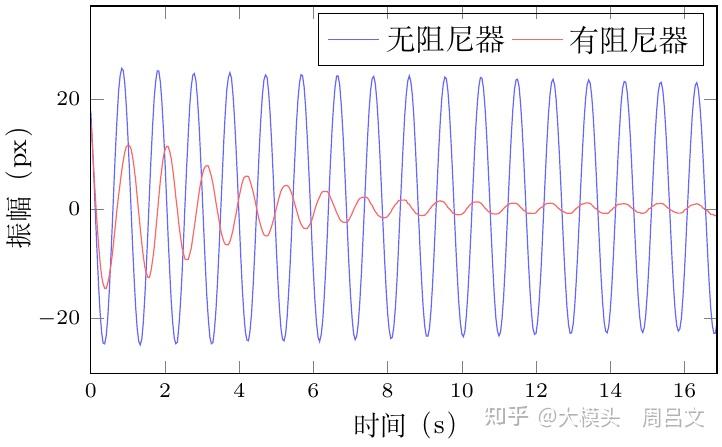
我们可以通过简单的视频图像处理，从实验视频（图 11 和 12）中获取有无阻尼器情况下主结构的振动情况，结果分别如图 13 和 14 所示。

图 14: 摆式调谐质量阻尼器实验结果

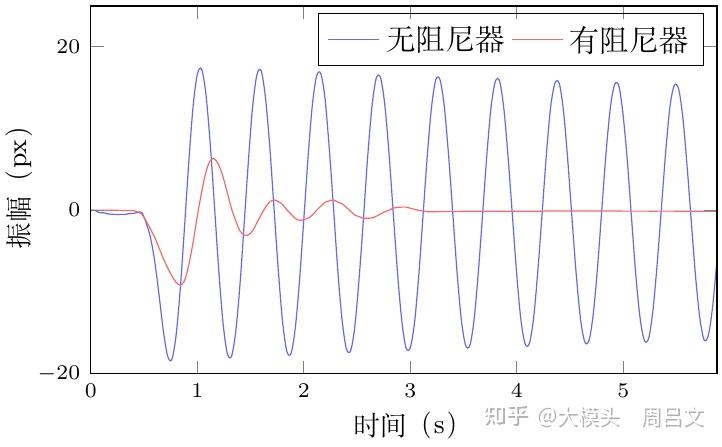
从两实验的振动曲线中都可以看出：在无阻尼器情况下，主结构的振幅衰减很慢，需要数十秒时间才能停止振动；而有阻尼器情况下，主结构的振幅迅速衰减，很快便停止了摆动。

模型

平移阻尼器是由安装在主结构中的质量块和阻尼弹簧构成（图 15）。质量块的振动频率被调整为与主结构共振频率相近，同时质量比主结构小得多。通过将主结构振动的部分能量传递给质量块和阻尼弹簧系统并由阻尼耗散掉，来减小主结构的振动。

图 15: 平移调谐质量阻尼模型

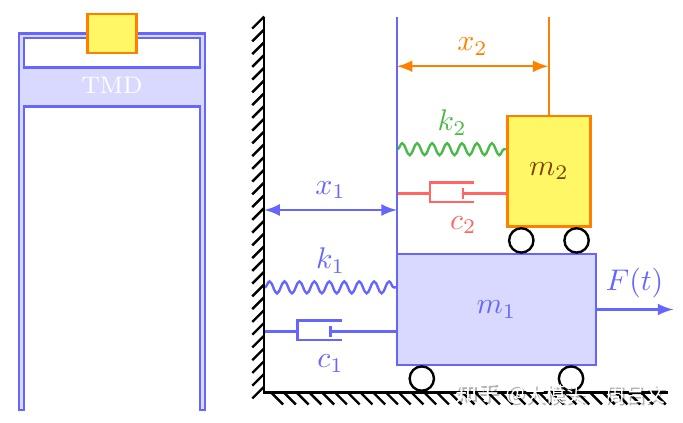
摆式阻尼器和平移阻尼器在原理上并没有本质区别（图 16）。为避免冗余，同时考虑到台北 101 的风阻尼器属于摆式，本文在接下来的模型中仅讨论摆式阻尼器。

图 16: 摆式调谐质量阻尼模型

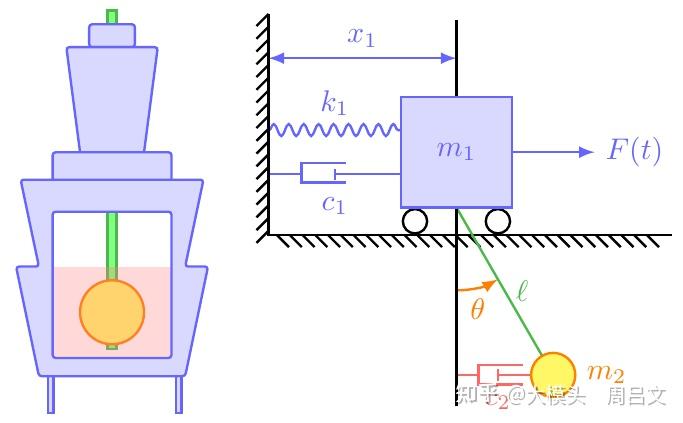
配有摆式阻尼器的大楼可以简化为一个受驱阻尼振子（大楼）和一个带阻尼的摆（阻尼器）。接下来，本文先分别分析一下阻尼谐振子和阻尼摆，然后再将阻尼谐振子和阻尼摆耦合起来模拟配有摆式阻尼器的大楼。

主结构

如果没有阻尼器，主结构（大楼）可以简化为如图 17 所示的阻尼谐振子[6]，其质量为 $m_1$ ，弹簧系数为 $k_1$ ，阻尼系数为 $c_1$ 。

图 17: 阻尼谐振子受力分析

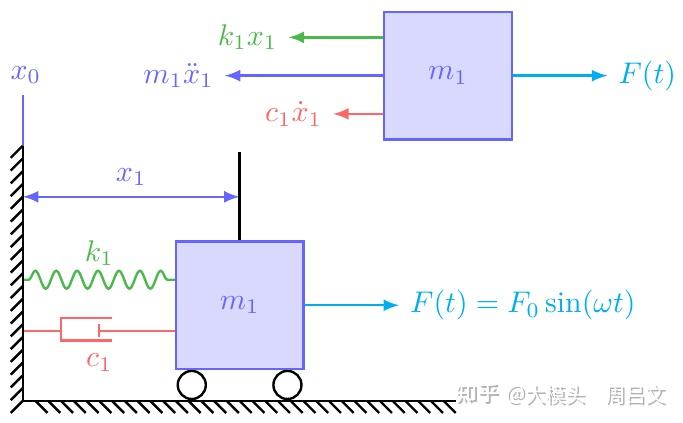
如图 17 所示，基底位置、速度和加速度分别为 $x_0$ 、 $\dot{x}_0$ 和 $\ddot{x}_0$ 。振子相对于基底位移为 $x_1$ ，速度和加速度分别为 $\dot{x}_1$ 和 $\ddot{x}_1$ 。对振子进行受力分析，并虚加上惯性力。除了周期性的驱动力 $F(t)$ 外，振子还受到弹簧回复力 $k_1 x_1$ ，阻尼力 $c_1 \dot{x}_1$ ，以及惯性力 $m_1\ddot{x}_1$ 。应用达朗贝尔原理，振子在形式上满足受力平衡：

$F(t) - m_1\ddot{x}_1-c_1 \dot{x}_1-k_1 x_1 = 0 \\$

其中 $F(t)$ 模拟风或地震对大楼的作用。如果仅考虑地震，即基底的速度和加速度不为零， $F(t)$ 的形式可假设为 $F(t)$ = - $m_1\ddot{x}_0$ ，其中 $x_0$ = $X_0\sin(\omega t)$ 。如果仅考虑风的作用， $F(t)$ 的形式可假设为 $F(t)$ = $F_0\sin(\omega t)$ ，其中 $F_0$ 为风作用在大楼上力的幅值。本文模型仅讨论风的作用（即 $x_0\equiv 0$ ），因此振子的运动方程为

$\ddot{x}_1 +2\xi_1\omega_1\dot{x}+\omega_1^2 x_1 = \frac{F_0\sin(\omega t)}{m_1} \\$

其中 $\xi_1$ = $c_1$ / $2\sqrt{k_1m_1}$ 为系统的阻尼比（系统的阻尼相对于临界阻尼的比值）， $\omega_1$ = $\sqrt{k_1/m_1}$ 为系统（无阻尼状态下的）固有频率。该方程可由龙格库塔法数值求解。

图 18: 主结构运动方程数值解

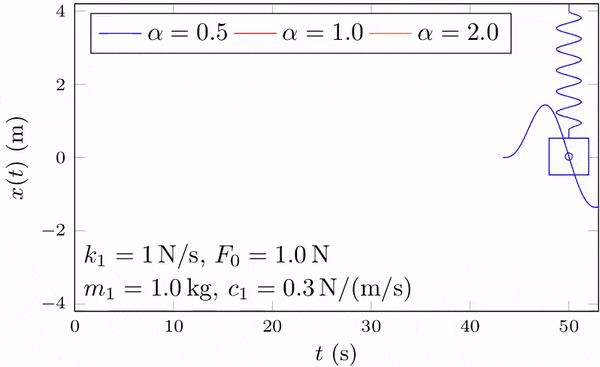
图 18 为三种频率比（ $\alpha$ = $\omega$ / $\omega_1$ ）下的求解结果，初始条件为 $x_1$ ( $t$ = 0) = 0， $\dot{x}_1$ ( $t$ = 0) = 0，求解所使用的其它参数值已经标注在图中。从图中可以看出，当驱动力频率与系统固有频率相等（ $\alpha$ = 1）时，振动幅度将越来越大，最终将以较大的振幅振动。而驱动力频率是系统固有频率 2 倍或 1/2 时，振幅小得多。当时间足够长，系统将达到稳定状态（周期性运动），系统的稳态解可表示为[7]

$x_1(t) = X_1\sin(\omega t -\phi_1) \\$

上式中的 $X_1$ 和 $\phi_1$ 分别为振幅和相位：

$\begin{aligned} X_1 &= \frac{F_0/k_1}{\sqrt{(1-\alpha^2)^2+(2\xi_1 \alpha)^2}}\\ \phi_1 &= \tan^{-1}\left(\frac{2\xi_1 \alpha}{1-\alpha^2}\right) \end{aligned} \\$

其中 $F_0/k_1$ 为振子在恒力 $F_0$ 作用下的静态位移， $\alpha$ = $\omega$ / $\omega_1$ 表示驱动力频率与系统固有频率之比。由振幅表达式可以看出，振子的振幅除了与自身弹簧系数、固有频率和阻尼比相关外，还与驱动力大小和频率相关。驱动力越大，振子的振幅越大。这一点不难理解：风越大，楼晃得越厉害。驱动力频率与系统固有频率越接近，振子的振幅越大，这就是所谓的“共振”效应。

图 19: 振幅与驱动力频率的关系

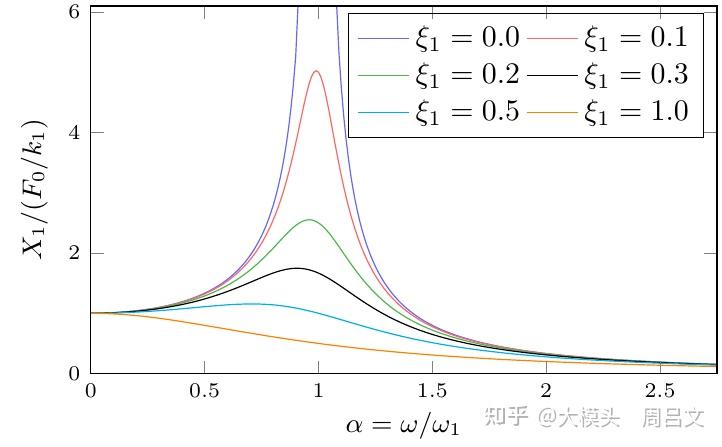
图 19 给出了不同阻尼比情况下，振幅与驱动力频率的关系。从图中可以看出，如果大楼的阻尼比较小，当风产生的激励频率与大楼的固有频率接近或相等时，大楼的晃动幅度将变得非常大。

图 20: 相位与驱动力频率的关系

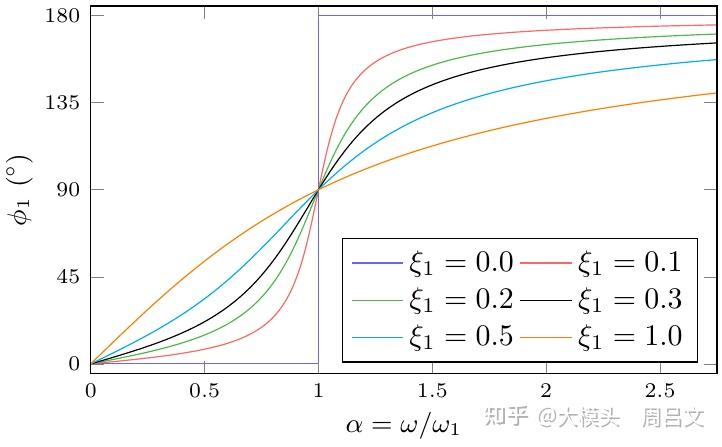
图 20 给出了相位与驱动力频率的关系。当 $\alpha$ = 1 时，振动与驱动频率的相位相差 90 $^\circ$ ，这对于确定系统的固有频率非常有帮助。当 $\alpha$ $\gg$ 1 时，振动与驱动频率的相位相差 180 $^\circ$ ；当 $\alpha$ $\ll$ 1 时，振动与驱动频率相位相同。

阻尼摆

摆式阻尼器可以简化为一个带有阻尼的单摆（图 21）。摆球质量为 $m_2$ ，摆线长 $\ell$ ，阻尼系数为 $c_2$ ，阻尼只限制摆球的水平运动。

图 21: 阻尼摆受力分析

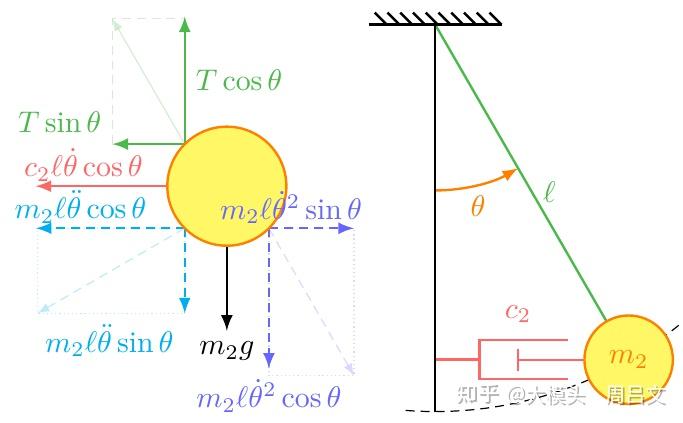
以摆球为研究对象，作受力分析（图 21），并虚加上摆球的惯性力。其中 $T$ 为摆线的张力， $c_2\ell\dot{\theta}\cos\theta$ 为阻尼力， $m_2\ell\ddot{\theta}$ 为垂直摆线方向的惯性力， $m_2\ell\dot{\theta}^2$ 为沿摆线方向的惯性力。应用达朗贝尔原理，摆球在形式上满足受力平衡：

$\begin{aligned} m_2\ell\left(\dot{\theta}^2\sin\theta - \ddot{\theta}\cos\theta \right)&-T\sin\theta -c_2\ell\dot{\theta}\cos\theta = 0\\ - m_2\ell\left(\dot{\theta}^2\cos\theta + \ddot{\theta}\sin\theta\right)&+T\cos\theta - m_2 g\quad\quad\,=0 \end{aligned}\\$

由以上两式消去 $T$ 后可得摆球的运动方程

$\ddot{\theta} + \frac{c_2}{m_2} \dot{\theta}\cos^2\theta + \frac{g}{\ell} \sin\theta = 0 \\$

通常情况下，摆球只在平衡位置小幅度摆动，因此 $\theta$ 较小。将 $\cos\theta$ $\approx$ 1， $\sin\theta$ $\approx$ $\theta$ 代入，上式可转化为以下齐次常系数微分方程[8]

$\ddot{\theta} + 2\xi_2\omega_2 \dot{\theta} + \omega_2^2 \theta = 0 \\$

其中 $\xi_2$ = ( $c_2$ /2 $m_2$ ) $\sqrt{\ell/g}$ 为系统的阻尼比， $\omega_2$ = $\sqrt{g/\ell}$ 为系统（无阻尼状态下）的固有频率。如果 $\xi_2$ = 0，即不考虑阻尼，上式就退化为单摆振动方程。

图 22: 阻尼摆模拟结果

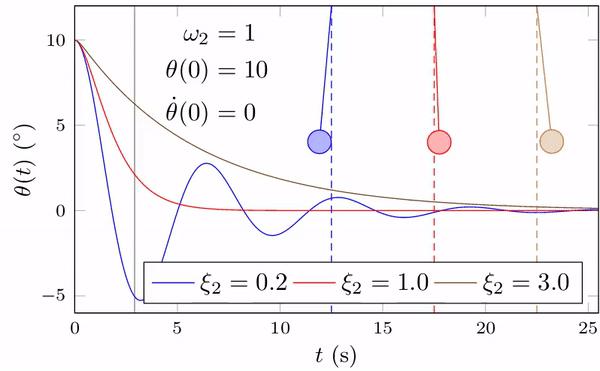
如果 $\xi_2$ $\neq$ 0，系统的行为将由 $\xi_2$ 和 $\omega_2$ 两个参数决定：当 0 < $\xi_2$ <1、 $\xi_2$ =1 或 $\xi_2$ >1 时，系统的阻尼形式分别表现为欠阻尼、临界阻尼和过阻尼（图 22），相应的解见附录。

主结构和阻尼摆耦合

配有摆式阻尼器的大楼可以看成阻尼振子和阻尼摆组成的系统，两者通过摆线 $\ell$ 和阻尼 $c_2$ 连接（图 23）。

图 23: 摆式调谐质量阻尼模型受力分析

在此情况下，振子不仅受到图 17 中的力，还受到摆线的拉力 $T\sin\theta$ （只考虑水平方向），和阻尼力 $c_2\ell\dot{\theta}\cos\theta$ 。因此其形式上的平衡方程变为

$T\sin\theta+ c_2\ell\dot{\theta}\cos\theta + F(t) - m_1\ddot{x}_1-c_1\dot{x}_1-k x_1 = 0 \\$

以振子（大楼）为参考系，摆球不仅受到图 21 中的力，还受到水平惯性力 $m_2\ddot{x}_1$ 。因此其形式上的平衡方程变为

$\begin{aligned} m_2\ell\left(\dot{\theta}^2\sin\theta - \ddot{\theta}\cos\theta \right)&-T\sin\theta -c_2\ell\dot{\theta}\cos\theta - m_2\ddot{x}_1= 0\\ - m_2\ell\left(\dot{\theta}^2\cos\theta + \ddot{\theta}\sin\theta\right)&+T\cos\theta - m_2 g\qquad\qquad\quad\;\; =0 \end{aligned}\\$

由以上三式可以求出阻尼振子和阻尼摆的振动方程：

$\begin{aligned} \ddot{x} &= +\frac{ F(t) - kx -c_1\dot{x} + m_2 g \sin\theta\cos\theta + c_2\ell\dot{\theta}\cos^3\theta + \ell m_2\dot{\theta}^2\sin\theta }{ m_1 + m_2(1-\cos^2\theta) }\\ \ddot{\theta} &= -\frac{( F(t)-c_1\dot{x}-kx+\ell m_2 \dot{\theta}^2 \sin\theta )\cos\theta + (m_1/m_2+1) ( c_2\ell\dot{\theta}\cos^2\theta + m_2g\sin\theta) }{ m_1\ell + m_2\ell(1-\cos^2\theta) } \end{aligned} \\$

考虑到 $\theta$ 和 $\dot{\theta}$ 是小量，将 $\sin\theta$ $\approx$ $\theta$ ， $\cos\theta$ = 1， $\dot{\theta}^2$ = 0 代入，同时令 $x_2$ = $\theta\ell$ ， $\dot{x}_2$ = $\dot{\theta}\ell$ ， $\ddot{x}_2$ = $\ddot{\theta}\ell$ ，则以上两式可改写为（具体推导过程见附录）

$\begin{aligned} \ddot{x}_1 &= + \frac{F(t)}{m_1} - \omega_1^2 x_1 -2\xi_1\omega_1\dot{x}_1 + \mu w_2^2 x_2 + 2\mu \xi_2\omega_2\dot{x}_2 \\ \ddot{x}_2 &= -\frac{F(t)}{m_1} + \omega_1^2 x_1 + 2\xi_1\omega_1\dot{x}_1 - (1+\mu) w_2^2 x_2 - 2(1+\mu) \xi_2\omega_2 \dot{x}_2 \end{aligned} \\$

其中 $\mu$ = $m_2$ / $m_1$ 为振子和摆球质量之比， $\omega_1$ = $\sqrt{k_1/m_1}$ 和 $\xi_1$ = $c_1$ /2 $\sqrt{k_1m_1}$ 分别为阻尼振子的固有频率和阻尼比， $\omega_2$ = $\sqrt{g/\ell}$ 和 $\xi_2$ = ( $c_2$ / $2m_2$ ) $\sqrt{\ell/g}$ 分别为阻尼摆的固有频率和阻尼比。注意，以上两式与平移阻尼器的运动方程形式一致（具体见附录）。以上方程可由龙格库塔法数值求解，图 24 为求解得到的有无阻尼器情况下主结构振动曲线。

图 24: 摆式调谐质量阻尼器模拟结果

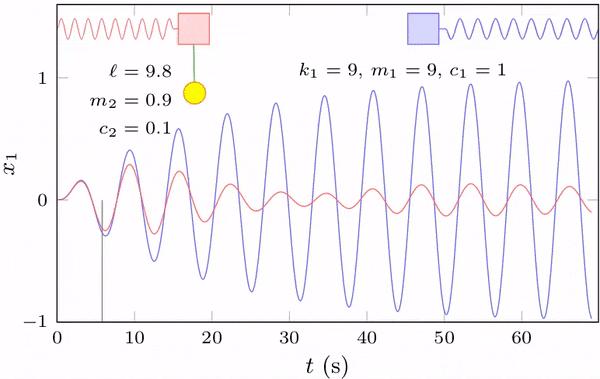
当时间足够长，系统将达到稳定状态（周期性运动），系统的稳态解可表示为：

$\begin{aligned} x_1(t) &= X_1\sin(\omega_1t -\phi_1),\qquad\, \;\;X_1 = \frac{F_0}{k_1}\cdot\frac{\sqrt{A^2+B^2}}{\sqrt{C^2+D^2}},\;\; \phi_1 = \tan^{-1}\left(\frac{A}{B}\right)\\ x_2(t) &= X_2\sin(\omega_2t -\phi_1+\phi_2),\;\; X_2 = \frac{F_0}{k_1}\cdot\frac{\alpha^2}{\sqrt{C^2+D^2}},\;\; \phi_2 = \tan^{-1}\left(\frac{C}{D}\right) \end{aligned} \\$

其中 $A$ = 2 $\xi_2$ $\alpha$ $\beta$ ， $B$ = $\beta^2$ - $\alpha^2$ ， $C$ = 2 $\xi_1$ $\alpha$ ( $\beta^2$ - $\alpha^2$ ) + 2 $\xi_2$ $\beta$ $\alpha$ (1 - $\alpha^2$ (1 + $\mu$ ))， $D$ = (1 - $\alpha^2$ )( $\beta^2$ - $\alpha^2$ ) - $\mu$ $\beta^2$ $\alpha^2$ - 4 $\xi_1$ $\xi_2$ $\beta$ $\alpha^2$ 。 $\mu$ = $m_2$ / $m_1$ 为摆球与振子的质量比， $\alpha$ = $\omega$ / $\omega_1$ 为激励频率与振子固有频率比， $\beta$ = $\omega_2$ / $\omega_1$ 为阻尼摆与振子的固有频率比。

优化阻尼器，实质上就是通过调整阻尼器与主结构质量比 $\mu$ 、阻尼器与主结构固有频率比 $\beta$ 、以及阻尼器的阻尼比 $\xi_2$ ，来最大程度地降低各种激励下主结构振幅 $X_1$ 的峰值。摆球质量 $m_2$ 应尽可能的大，以提高质量比 $\mu$ 。但 $m_2$ 的最大值通常由主结构（大楼）决定的，在绝大多数结构中，质量比都不超过 0.1。因此，优化阻尼器主要通过调整 $\beta$ 和 $\xi_2$ ，图 25 是不同 $\beta$ 和 $\xi_2$ 下的主结构振幅。

图 25: 不同参数（$\xi_1=0.05$）下的主结构振幅

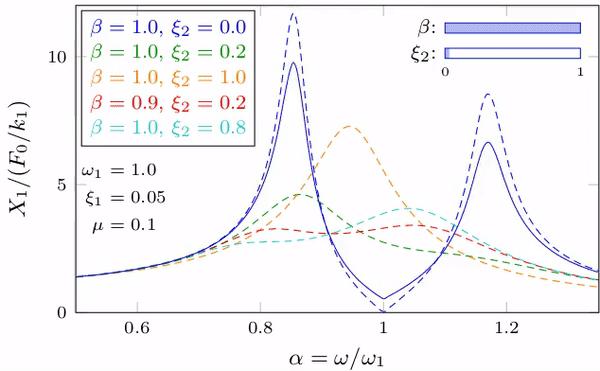
从振幅 $X_1$ 表达式或图 25 都可以看出，当 $\xi_2$ = 0 且 $\beta$ = 1 时，主结构在 $\alpha$ = 1 时不仅不发生共振，而且是完全不振动。这看起来很完美，但振幅曲线会出现两个新的峰值（蓝线）。风对大楼的作用频率并不是固定不变的，因此 $c_2$ = 0 且 $\omega_2$ = $\omega_1$ 的设置并不合适。但这种设置也不是一无事处，例如当工厂的机械总是以固定的频率振动时，可以用这种设置来减振。从图 25 中的红线可以看出，通过调整阻尼器的阻尼比 $\xi_2$ ，以及阻尼器与主结构固有频率比 $\beta$ 可以大幅度有效地降底主结构峰值。

图 26: 不同参数（$\xi_1=0$）下的主结构振幅

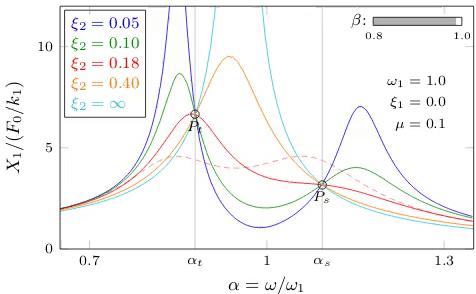
通常主结构的阻尼比较小（如果很大就不用安装阻尼器了）。如果忽略主结构的阻尼（即认为 $\xi_1$ = 0），会发现同一个 $\beta$ 值下的所有振幅曲线都经过相同的两点 $P_t$ 和 $P_s$ （图 26）。当且仅当 $P_t$ 和 $P_s$ 两点高度相等且为振幅曲线上的最高点时，振幅曲线峰值最小（红色虚线），相应的阻尼器最优频率和阻尼比为（具体推导过程见附录）

$\begin{aligned} \omega_2^\mathrm{o} &= \sqrt{\frac{g}{\ell^\mathrm{o}}}=\frac{\omega_1}{1+\mu}\\ \xi_2^\mathrm{o} &= \frac{c_2^\mathrm{o}}{2m_2}\sqrt{\frac{\ell^\mathrm{o}}{g}}= \sqrt{\frac{3\mu}{8(1+\mu)}} \end{aligned}\\$

在此情况下，振幅曲线的峰值为

$X_2^\mathrm{o} = \frac{F_0}{k_1}\sqrt{1+\frac{1}{\mu}} \\$

从上式中可以看出，阻尼器与主结构质量比 $\mu$ 越大，振幅曲线的峰值越小。综上所述，如果忽略摩天大楼自身的阻尼比，则为其设计摆式风阻尼器的步骤如下：

在大楼承重允许范围内，最大化摆球质量 $m_2$ ，即最大化摆球与大楼的质量比 $\mu$ = $m_2$ / $m_1$ 。
通过调整摆线长度 $\ell$ = $\ell^\mathrm{o}$ ，使得摆式阻尼器的固有频率为最佳值 $\omega_2^\mathrm{o}$ 。
通过调整阻尼器的阻尼强度 $c_2$ = $c_2^\mathrm{o}$ ，使得阻尼比为最佳值 $\xi_2^\mathrm{o}$ 。

以上步骤同样适用于平移风阻尼器的设计。对于需要考虑自身阻尼比的摩天大楼，其风阻尼器的设计可在以上最优值基础上略作调整。注意，以上阻尼器的最优参数只适用于对主结构的简谐力激励（风）。如果外界激励改为基底简谐加速度（地震），阻尼器的最优参数表达式会略有变化[9]。

结果

本小节，我们将通过数值求解上文构建的振动方程来模拟台北 101 大楼的防风抗震。台北 101 大楼的自然振动周期约为 6.8 秒左右，摆球质量约为 660 吨，摆长约为 12 米[10]。在本文的模拟中，取塔楼的等效质量 $m_1$ = 1.4 $\times 10^7$ kg，弹簧系数 $k_1$ = 1.2 $\times 10^7$ N/m，阻尼系数 $c_1$ = 5.2 $\times 10^5$ Ns/m，摆球质量 $m_2$ = 6.6 $\times 10^5$ kg。模拟防风时对主结构施加简谐力，模拟抗震时对基底施加简谐加速度，两种激励的幅值分别为 $F_0$ = 3 $\times 10^6$ N 和 $X_0$ = 0.25 m。根据模型可得最优摆长和阻尼系数分别为 $\ell^\mathrm{o}$ = 12.4 m 和 $c_2^\mathrm{o}$ = 1.5 $\times 10^5$ Ns/m。注意，这里的 $m_1$ 、 $k_1$ 、 $c_1$ 和 $c_2$ 的取值可能与实际值相差甚远。原因主要有两方面：其一，这些参数值并不像摆长和摆球质量一样容易获取；其二，为了使模拟结果更具有差异性，本文故意放大了质量比。模拟过程中将不断加大外界激励的频率，观察大楼在不同激励频率下的振动情况。模拟还将对比不同摆球质量、摆长和阻尼系数的影响。

不同质量

首先，考虑不同摆球质量的影响。在其它参数值取最优的情况下，调整摆球质量分别为台北 101 摆球实际质量的 1/2、1 和 2 倍，并分别进行数值模拟。防风和抗震的模拟结果分别如图 27 和 28 所示。

图 27: 不同摆球质量的防风模拟

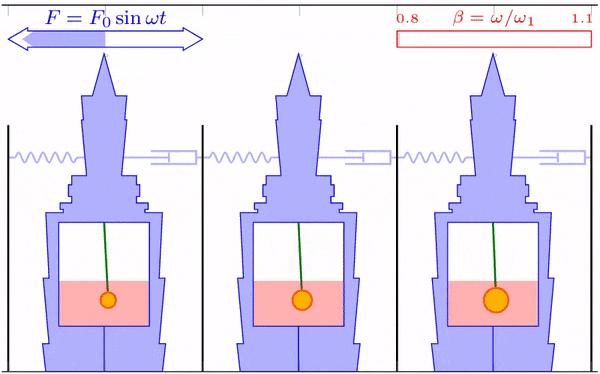
模拟显示，摆球质量越小，大楼和摆球的晃动幅度都越大。可以想像两种极端情况，当摆球质量趋近于 0 时，相当于没有阻尼器；当摆球质量无穷大时，别说晃楼了，连阻尼器都晃不动。

图 28: 不同摆球质量的抗震模拟

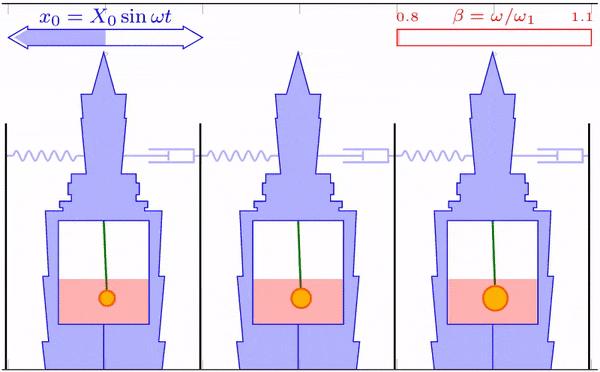
在防风模拟中，三种质量的最大振幅分别为 2.19、1.38 和 1.05 m。在抗震模拟中，三种质量的最大振幅分别为 2.24、1.39、1.06 m。和理论分析的一样，摆球质量越小，各种频率下大楼的最大振幅越大。因此，在为摩天大楼设计风阻尼器时，阻尼器的质量应尽可能大。但考虑到大楼的承载限制，阻尼器的质量还是有上限的。在之后的模拟中，使用与台北 101 摆球相同的质量作为摆球质量。

不同摆长

接下来，考虑摆长的影响，摆长直接决定了阻尼摆的自然摆动周期。在其它参数值取最优的情况下，调整摆长分别为台北 101 实际摆长的 1/3、1 和 3/2 倍，并分别进行数值模拟。防风和抗震的模拟结果分别如图 29 和 30 所示。

图 29: 不同摆长的防风模拟

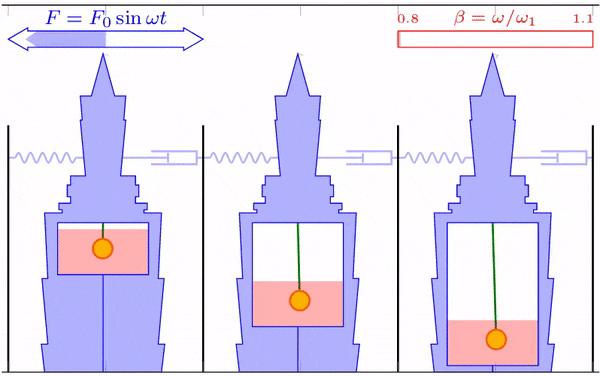
模拟显示，摆长过短或过长时，摆球的摆动幅度都不如最佳摆长大，而大楼的最大振幅却比最佳摆长时大。可以想像两种极端情况，当摆长趋近于 0 时，摆球直接固定在了大楼上，相当于没有阻尼器；当摆长无穷长时，摆的周期也变成了无穷大，也相当于没有阻尼器。

图 30: 不同摆长的抗震模拟

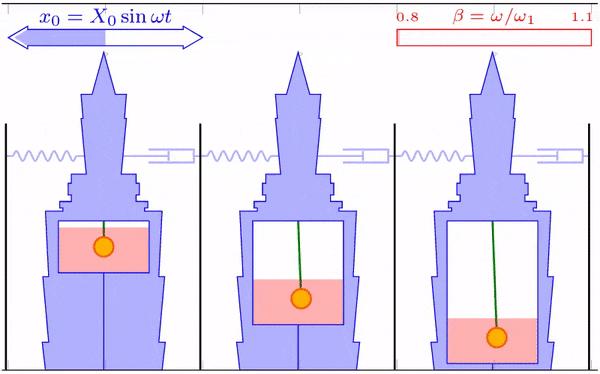
在防风模拟中，三种摆长的最大振幅分别为 4.32、1.38 和 2.67 m。在抗震模拟中，三种摆长的最大振幅分别为 4.37、1.39 和 2.66 m。模拟结果表明，两种激励下，摆长设置为最优值的 1/3 和 3/2 时，最大振幅分别是最优摆长的 3 倍和 2 倍。因此，适当的摆长确实能够有效地降低大楼的晃动幅度。

不同阻尼

最后，考虑阻尼摆阻尼大小的影响。在其它参数值取最优的情况下，调整阻尼分别为最优阻尼值的 1/4、1 和 4 倍，并分别进行数值模拟。防风和抗震的模拟结果分别如图 31 和 32 所示。

图 31: 不同阻尼的防风模拟

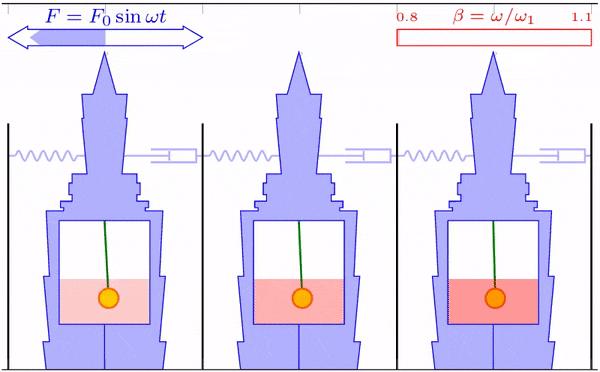
模拟显示，当阻尼值较小时，摆球摆动幅度较大，大楼的最大振幅也较大，但当激励频率等于大楼固有频率时，大楼几乎不晃了，取而代之的是摆球的剧烈摆动。当阻尼值较大时，摆球由于阻尼的作用，摆动幅度很小，大楼的最大振幅也较最优阻尼时大。可以想象两种极端情况，当完全没有阻尼时，就是图 25 中蓝线情况，大楼在外界激励等于其固有频率时完全不动，但会在固有频率前后各出现一个较大的振幅峰值；当阻尼无穷大时，摆球直接固定在了大楼上，相当于没有阻尼器。

图 32: 不同阻尼的抗震模拟

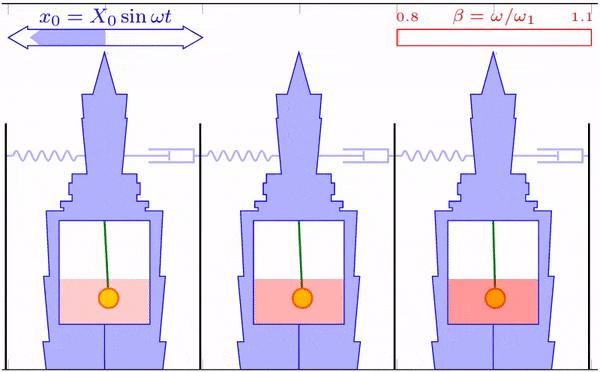
在防风模拟中，三种阻尼的最大振幅分别为 2.70、1.38 和 2.74 m。在抗震模拟中，三种阻尼的最大振幅分别为 2.74、1.39 和 2.78 m。模拟结果表明，两种激励下，阻尼设置为最优值的 1/4 和 4 倍时，最大振幅几乎都是最优阻尼的 2 倍。因此，适当的阻尼确实能够有效地降低大楼的晃动幅度。

结论

随着社会发展和技术进步，越来越多的摩天大楼出现在我们面前，摩天大楼也越建越高。防风抗震是大楼设计者要着重考虑的问题，通过在大楼中加入风阻尼器（调谐质量阻尼器）是目前较为常见且最为行之有效的方法之一。本文建立了调谐质量阻尼器的运动方程，对不同参数和外界激励频率下主结构振动情况进行了分析，并给出了阻尼器的最优参数。在此基础上，本文对台北 101 大楼进行了模拟，采用了两种激励来分别模拟并分析强风和地震时大楼的振动情况。模拟结果与理论分析以及实验一致：调谐质量阻尼器能够有效地降低摩天大楼在强风和地震中的晃动幅度。

参考资料

[1] SimScale GmbH. Burj khalifa wind speed contours (slice sections), 2019: https://www.youtube.com/watch?v=6BTmFMNrHhM

[2] Stefan Al. Will there ever be a mile-high skyscraper, 2019: https://www.youtube.com/watch?v=kF54-camgCg

[3] Practical Engineering. Tuned mass dampers in skyscrapers, 2016: https://practical.engineering/blog/2016/2/14/tuned-mass-dampers-in-skyscrapers

[4] TESolution. Principle of tuned mass damper(tmd) technology, 2016: https://www.youtube.com/watch?v=lhNjfNUOUo8

[5] Edd China. Vibration-damping technology by sandvik coromant, 2019: https://www.youtube.com/watch?v=VCxm3vTWgvU

[6] Wikipedia contributors. Vibration — Wikipedia, the free encyclopedia, 2021: https://en.wikipedia.org/wiki/Vibration

[7] Mustafa Arafa. Response of a damped system under harmonic force, 2007: http://www1.aucegypt.edu/faculty/mharafa/MENG%20475/Forced%20Vibration.pdf

[8] Wikipedia contributors. Damping — Wikipedia, the free encyclopedia, 2021: https://en.wikipedia.org/wiki/Damping

[9] G. B. Warburton. Optimum absorber parameters for various combinations of response and excitation parameters. Earthquake Engineering & Structural Dynamics, 10(3):381–401, 2010: https:

[10] L. L. Chung, Y. A. Lai, Cs Walter Yang, K. H. Lien, and L. Y. Wu. Semi-active tuned mass dampers with phase control. Journal of Sound & Vibration, 332(15):3610–3625, 2013: https:

上一篇：《天龙八部》里的慕容复为什么失败？

下一篇：疑似以色列远程操控黎巴嫩通讯设备引发爆炸导致数千人伤亡，这是如何做到的？

END