高中数学圆锥曲线怎么学，做题才能得心应手?

写在前面：

看了下你这个娃娃的问题和需求：

总结一下：

嗯，说实话，如果有这样的方法，我也想学．

因为在任何一章中，通法和特法的特点都是相对固定的：

通法：适用范围广，但一般比较耗时间；
特法：简捷快速，但技巧性强、适用范围也窄．

没有方法，可以只要二者的优点，而摒弃二者的缺点．如果有，那就是做题者已经达到了“得心应手”的阶段了．

---

孔子在《论语 为政》中写道：

【原文】子曰：“吾十有五而志于学，三十而立，四十而不惑，五十而知天命，六十而耳顺，七十而从心所欲，不逾矩．”
【译文】孔子说：“我十五岁就立志学习，三十岁能够有所成就，四十岁遇到事情不再感到困惑，五十岁就知道哪些是不能为人力支配的事情而乐知天命，六十岁时能听得进各种不同的意见，七十岁可以随心所欲（收放自如）却又不超出规矩．”

看了你的提问，你现在的状态有可能处于这样的阶段：二级结论还没有记很牢（虽然我们不推荐直接记忆），而且在通法上的熟练度也不够．

如果此时想要到达“得心应手”的程度，无异于想直接从“有志于学”到达“从心所欲，不逾矩”的阶段．这一点，即使是“圣人”，他也难办呀... ...毕竟，圣人自己，也是经历了“而立”、“不惑”、“知天命”、“耳顺”这几个阶段，才达到“从心所欲，不逾矩”（得心应手）的阶段的．

至于如何破局？

其实“魔法棒”已经在你手中了，就是你现在的知乎名：

循序渐进．

【1】先通过老师讲解//参考书梳理//自己做题等方式，总结出常考的题型．把常考题型的通法练习熟练，即使运算量大，也要坚持算完．
一者，圆锥曲线解答题的两个重难点就是：思维和运算；
二者，目前的高考对运算要求并不低．
【2】在练习通法的同时，针对特定的题型，适当地提炼和总结经验（或者直接记住老师//参考书给的，然后自己再结合具体的题目进行推导和适用），形成所谓的结论．
【3】在通法和结论都烂熟于心的情况下， 因题制宜，就可以得心应手，找到更优（甚至最优）的解题思路．

不妨结合刚写的一个专题，来示范下如何进行这样的学习：

木兰诗中有兔子：圆（6）：【专题】切线方程和切点弦方程

一、十五而有志于学（想要学好）

比如，圆/椭圆/双曲线/抛物线的切线方程和切点弦方程系列，在教科书上有相关的题目，但并没有给出明确的专题，更没有给出相关的结论．

但是，在平时考试和高考中，却会时常见到它们的身影．

如你所说，在这个系列中（圆锥曲线的缩影）：

有通法，比如，“联立法”和“求导法”．这两种的任何一种，对于椭圆/双曲线来说，运算量都挺大的；
有特法，比如，它们四个都有相关的结论可以记忆，但解答题中却又无法直接使用．

假设现在，我们的目标是“熟练解决这个系列”，就像你想要的：“针对每道题，找到更优的解题思路”．

二、三十而立（有所成就）

那么，第一步要做的，就是先把各种可用的方法梳理出来，逐个练习清楚．

比如，过圆上一点的切线方程的计算：

我们提供了六种方法，你需要做的就是把每一种方法理解清楚，然后练习熟练（就是... ...全都要练熟）：

为什么要学习那么多种方法？

因为你要快速找到“更优//最优的路”，你首先脑子里需要储备“所有的路（或大部分路）”．

比如，一个题目问：“杜甫的那首诗表现了他忧国忧民的思想？”

要回答得很好，起码你需要知道杜甫都写过哪些诗，然后才能快速地找到相应的诗．

比如，一个同学问：“导数与三角函数的综合题有什么解题技巧？”我只能说，没有技巧（但有方法）．

要想很好地解决这类题目，做题者需要掌握的是“导数与三角函数综合的题型”可用的方法，然后根据具体的题目选用（因为有的题目适合甲方法，有的题目适合乙方法）．

导数与三角函数的综合问题有什么解题技巧?

比如，我们只是想很好地解决圆锥曲线中的“轨迹”这一个系列，都需要对整个轨迹的题型和解决方法都烂熟于心．

木兰诗中有兔子：曲线轨迹之三十六计（1）：直接法求轨迹木兰诗中有兔子：曲线轨迹之三十六计（2）：定义法求轨迹木兰诗中有兔子：曲线轨迹之三十六计（3）：转移法求轨迹木兰诗中有兔子：曲线轨迹之三十六计（4）：参数法求轨迹木兰诗中有兔子：曲线轨迹之三十六计（5）：几何法求轨迹木兰诗中有兔子：曲线轨迹之三十六计（6）：交轨法求轨迹

然后才能灵活应用，才能进一步谈得上在多种方法中找到最合适的方法：

木兰诗中有兔子：曲线轨迹之三十六计（7）：实际应用与新定义木兰诗中有兔子：曲线轨迹之番外篇：中点弦轨迹之“分合”木兰诗中有兔子：曲线轨迹之番外篇：中点弦轨迹之“一览众山小”

现在中学生不是有句流行的话，是“你必须十分努力，才能看起来毫不费力”吗？

迁移到这里来，就是“你必须掌握所有的方法，才能快速找到那道题目最合适的方法”．

三、四十而不惑（不再因不同的题型困惑）

掌握了这六种方法之后，然后再想想：如果把“圆”变成“椭圆、双曲线和抛物线”，又有哪些方法可用，哪些方法不可用？

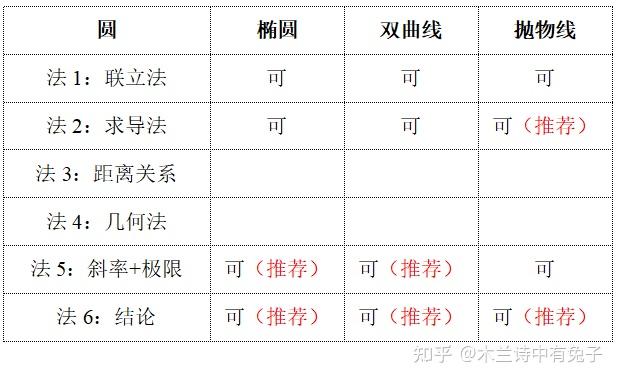
那么，当你遇到椭圆/双曲线/抛物线的相关题目时，就不再会“迷惑”了．

四、五十而知天命（知道无法干涉试题的出法）

刚刚掌握好“过曲线上一点的切线方程”，又来了一类“过曲线外一点的切点弦方程”．

没办法，我们无法干涉“试卷出什么题”这个“客观事实”，所以只能提高我们的解题和应对能力了．

所以，继续．

先掌握适用于圆/椭圆/双曲线/抛物线的通法，然后再单独掌握适用于圆的特法．

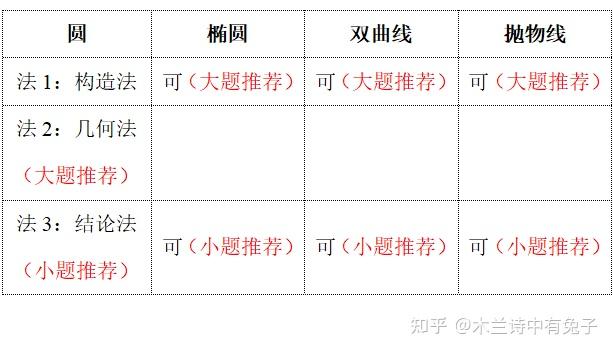
五、六十而耳顺（坦然接受各种出法）

熟练掌握了各种通法和特法后，随便题目怎么出，即使是以我们少见的或者“新定义”形式出现，我们也会很坦然了．

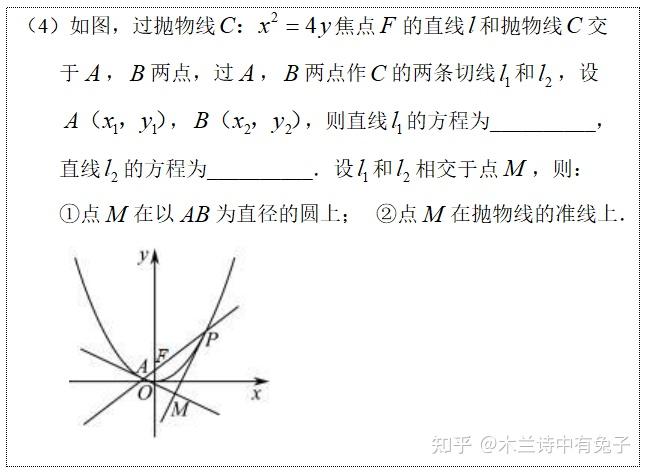
六、七十而从心所欲，不逾矩（得心应手）

因为不管它出“圆”，还是“椭圆/双曲线”，或者是“抛物线”；不管它是出“切线方程”还是“切点弦方程”；不管它是出选填，还是解答... ...

我们都可以看完题目后，就迅速定位到最适合这道题的方法，并且还可以不丢分．

如此，才有可能达到你说的“得心应手”的程度．

总结一下，就是学习如登山，有方法但无捷径．

老师（很广， 可以是学校老师、辅导资料、网络素材、甚至你不停练习和总结的自己）就是先你几步登上山顶的人．

因为很多时候，单靠自己的摸索和试探去登山，既耗费时间，还可能不安全．所以好的老师，会把登山的路线图、一些省力小技巧、某些地方可能遇到的风险、相应的处理方法等，用清晰简单的方式传授给你，辅助你快速找到最合适的路，以更安全更高效的方式登上去．

但是，要想登上山顶，除了自己一步一步地攀登之外，别无他法．

小彩蛋：

附录另一个同学的类似的问题：

如何从像庖丁解牛一样去解决高中数学？

祝更上一层楼~