DID(双重差分)该如何系统地学习?

发布时间：

2024-08-01 11:25

阅读量：

PRE

在上一章我们介绍了准实验设计中，一种常用的避免内生变量影响的回归方法--工具变量法IV。

叫我阿哲就好：因果推断（三）--工具变量法（IV）

在这一节，我们再来介绍准实验设计中，一种常用的消除组间差异的方法--双重差分法（Difference-in-Differences，DID），该方法提供了一种非常常用的分析思路，可以广泛的应用在实验分析中，整体思想比较简单、易于理解。

核心思想

时间的流逝会使问题变得更加复杂，随着研究从实验的干预前阶段进展到干预后，时间的自然流逝都将以潜在的方式改变观察变量的表现，而DID回归模型可轻松求解类似问题，创造出消除差异、公平对比的环境。

由于双重差分思想较为简单，我们举一个例子就能说明整套研究思路：

假如，我们拥有PA、NJ两组实验组，我们对这两组对象展开观察，由于用户组表现和时间序列有所关联，用户的表现状态随时间推移是逐渐下降的，在我们开始观察开始到进行干预的时间段之间，我们一般称之为AA期，即干预前的观察阶段：

1、在这个阶段我们主要通过观察样本表现是否会随时间变化，

2、两组实验组之间是否存在质的差异（即对照组和实验组可能并不是完全同质的）

那么这个时候我们就面临两个问题，一个是如何消除时序的影响，另一个就是如何消除组间差异：

DID的核心思想非常简单，他假设两组实验组在外部条件一致的情况下，随时间变化的趋势是一致的，这一点我们称之为平行趋势假设；

这一点非常重要，如果观察到趋势并不一致或非线性，那么需要采取其他的处理手段；

基于趋势一致的假设前提条件下，我们的干预效果就可以表示为：[Y(D)-Y(E)]-[Y(A)-Y(C)]

DID举例

简而言之，就是AB期差异减去AA期组间自带的差异，平行趋势假设意味着，如果没有干预，干预组和对照组之间的差异将保持不变（B点）。

这样一来，通过简单进行两次差分，就可以评估出干预效果，但在这里尤为重要的是两个实验组在AA期是否平行，趋势是否一致；

通常情况下，我们会采用一种伪干预测试的方法，即将AA期再次进行拆分，假设在该阶段某时间点实行了干预，实验前后是否存在显著差异。

非平行趋势

针对于非平行趋势，我们在后续文章中，会进一步介绍如何使用其他方法（如合成控制法）来解决这个问题。

基本原理

在了解了DID的工作流程及核心思想后，我们在简单介绍一下其背后的数学原理，综合起来理解可能效果会更好。

首先我们再来回顾一下，什么是准实验设计？
准实验设计是一种没有真正随机化过程的实验设计。由于缺乏随机分配，治疗组和对照组在干预前并不相同。因此，这两组之间的任何差异都可能是由预先存在的差异造成的。准实验的结果不会像 A/B Test那样精确，但我们希望能对因果关系进行合理的解读。

接下来我们详细介绍DID背后的数学思想。

下面的等式说明了 DID 模型的结构：

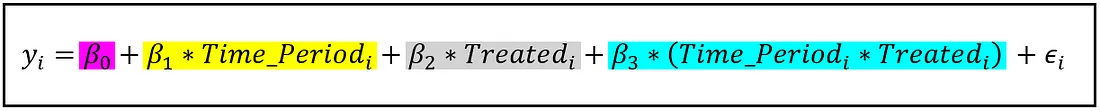
$y_i=\beta_0+\beta_1*Time_i+\beta_2*Treated_i+\beta_3*(Time_i*Treated_i)+\epsilon_i$

DID回归模型

上述等式就是DID回归模型的通用表达方式，其中：

$y_i$ 就是表示第i个观察值的响应变量（测量值）；

$\beta_0$ 表示回归截距；

$Time_i$ 可以理解为示性变量，取0或1，表示当前测量值是干预前还是干预后；

$Treated_i$ 同样表示为示性变量，取0或1，表示当前观察样本是干预组还是对照组的样本；

$\epsilon_i$ 表示第i个样本的误差项，捕捉模型无法表示的其他影响；

由模型中两个虚拟变量影响，我们模型的表现形式分为2*2 种，分别表示为：

由此，我们可以得到干预前后两组实验组的差异，即响应变量 $y_i$ 的差异表示：

对于干预组来说，干预前后的期望差异可以表示为：

$E[y_i|Time_i=1,Treated_i=1]-E[y_i|Time_i=0,Treated_i=1] \\ =(\hat{\beta_0}+\hat{\beta_1}+\hat{\beta_2}+\hat{\beta_3})-(\hat{\beta_0}+\hat{\beta_2}) \\ =(\hat{\beta_1}+\hat{\beta_3})$

同样的，对于对照组来说，干预节点（对照组不涉及干预策略）前后的期望差异可以表示为：

$E[y_i|Time_i=1,Treated_i=0]-E[y_i|Time_i=0,Treated_i=0] \\ =(\hat{\beta_0}+\hat{\beta_1})-\hat{\beta_0} \\ =\hat{\beta_1}$

此时，两组差异之间的差异就表示出了干预对干预组的影响效应：

$E[Effect] = (\hat{ \beta_1 }+ \hat{\beta_3})-\hat{\beta_1} =\hat{\beta_3}$

而 $\hat{\beta_3}$ 正是我们DID模型结构中交叉项Time*Treated)的系数估计。

在训练完 DID 模型后，交互项的拟合系数将为我们提供我们正在寻找的估计差异效应。系数相应的 p 值将告诉我们该效应是否显著，以及构建我们想要的置信区间。

以下为一个python实例：

import pandas as pd import numpy as np import statsmodels.api as sm

data = { 'store' : [ 'A' ]* 11 + [ 'B' ]* 11 , 'year' : np.concatenate([years]* 2 ), 'sales' : np.concatenate([store_A_sales_1, store_A_sales_2, store_B_sales]) } df = pd.DataFrame(data) df[ 'year' ] = df[ 'year' ].astype( int ) # 创建干预指示变量 df[ 'treatment' ] = (df[ 'store' ] == 'A' ).astype( int ) # 创建时间指示变量 df[ 'post' ] = (df[ 'year' ] >= 2015 ).astype( int ) # 创建交互项 df[ 'treatment_post' ] = df[ 'treatment' ] * df[ 'post' ] # 使用 OLS 回归执行DID分析 X = df[[ 'treatment' , 'post' , 'treatment_post' ]] X = sm.add_constant(X) # 添加截距常数项 y = df[ 'sales' ] # 拟合 OLS 模型 model = sm.OLS(y, X).fit() # 打印回归结果 print (model.summary())

End

经过上述的介绍，我们可以发现DID原理较易理解，且实际应用操作较为简单，因此该方法更多情况下是作为一种分析思想应用在各个场景中，通过双重差分能够有效控制那些不随时间变化的未观测因素的影响。这使得DID能够在许多情况下比简单的前后对比或处理组和对照组的对比更加可靠。

但是受限于平行趋势强假设，业务场景存在局限性，在后续我们将介绍更多方法，求解对应的特殊场景。

上一篇：为什么小米电视突然就没人关注了？

下一篇：为什么有人会以为自杀是一种解脱?

END