高三生,想考985,但数学最后两道压轴题感觉怎么刷题练习都解不出来,请问是放弃压轴还是坚持?
删教材的恶果。
还有很多知识点,高中学校没教,高考依然会考。拿着少掉几本的四书五经去科举,不砸才怪。
什么“打好基础”“夯实基础”,通通都是借口。因为少掉的那些知识点,导致一些本来很容易的题目就成了你自己去推那些常见二级结论。考试变成现场研究定理推论,考试的时候你能有多少时间从容静心去琢磨?
一些数学动不动就上140,拿下150的同学,其实不过学全了,有资源去补课把该考的东西都学完罢了。这跟什么天赋毫无关系。真有天赋那么厉害就去竞赛,数学联赛就是最好的试金石。
你做不出来那两道压轴题不奇怪,考的你压根就没学过没见过,人家补完的同学一眼就看到是“学过”的知识点,你只能两眼干瞪不知所云。
趁寒假赶紧去补,B站也好,百度网盘也好,赶紧去搜网课学全了,别指望学校那三瓜两枣。因为学校压根没教全。
第0篇高中学习方法攻略总纲分割线————————————————————
删了多少内容,以数学圆锥曲线为例。
公元前200年左右,古希腊,阿波罗尼奥斯《圆锥曲线论》,一己之力将圆锥曲线的性质和定理研究了个透彻。换个说法,现在高考考你的那些能算出人命的圆锥大题第二问,全是这本书上总结的内容。
好了,问题来了,笛卡尔(1596–1650)。而坐标系就是笛卡尔的贡献。
跨越接近19世纪的两个人,先不论国籍,代沟肯定是比天堂地狱还大。
然后这两位数学家就组成现在神奇的圆锥曲线大题。这种究极缝合怪,本来就不该存在。
两千多年前,阿波罗尼奥斯压根就没有坐标系,他那些圆锥曲线相关的结论,用的是几何证明。你没看错,就是跟欧几里得《几何原本》里面的那种几何证明,初中的时候平面几何题就能把几乎所有学生摁在地上摩擦。
不知道有多少同学知道真相会不会留下眼泪。如果用阿氏圆、准线,来考阿波罗尼奥斯,现场是这样:

如果现在高考让各位用纯几何做圆锥曲线大题第二问,不知道能疯几个?但纯几何这才是正统。建系去硬算那才是“歪门邪道“。
现在你们可以想象一下那个画面有多美了,原来圆锥大题其实是小众的初中平面几何证明题。在高中这种证明题也就数学联赛还有平面几何还有这种知识,你们看看下面的高联蜘蛛网大题感受下:
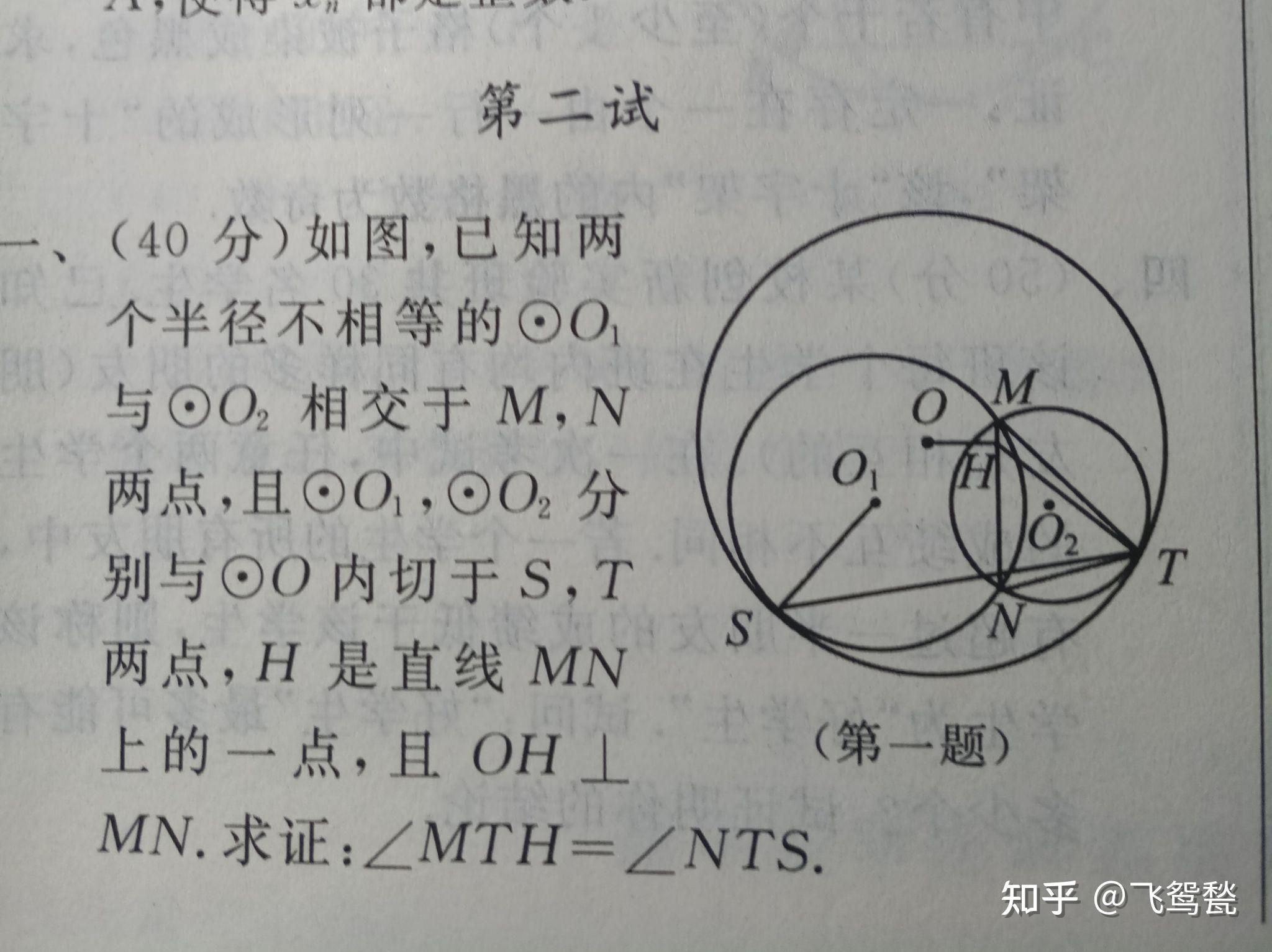
感觉看一眼就能让心理承受能力较弱的同学疯掉了。
小结:如果现在是有条件和资源搞数学竞赛的同学,并且在平面几何大题能够啃下来的同学当中,用纯几何去做圆锥曲线大题是毫无问题。
数学是一个连贯的学习进程:初中平几(欧几里得《几何原本》)→《圆锥曲线论》
这是一个完整连贯的过程,因为初中乃至高中的偷工减料,导致对圆锥曲线的理解本身都出现了问题。
笛卡尔坐标系的加入,影响了对数学的一些概念和形状的感知。这些要划重点:数学是感知,而不是计算。缺失了对美的感知,直接影响对数学的掌握。枯燥的硬算肯定会削弱对数学的兴趣。
现在联赛已经更新换代很多次,很多基础内容已经开始不教了,连竞赛教练都不教了,一般学校的老师可想而知。为了适应试题变化去削减教学内容,这就是为什么数学内部各个章节看起来居然可以割裂的原因,也是大家学来学去学不通的根本。缺失的内容不止平几→圆锥里面的纯几何部分,还有很多。
(分割线)——————————————————
好像说了很多无关的东西。题主那个问题要解决,唯一的办法就是补充很多本来必学的内容,在学完这些东西以后,自然而然就爬上130或者140了。而不是像一些答主说的那样要先爬到120才能慢慢爬向更高的分数。缺失的部分内容哪怕只是草草过一眼,也比你自己私下刷大量的题目管用,而且提分更加轻松容易。
区别就是学过没学过罢了。很多老师家长喊什么“基础不牢地动山摇”,实际该讲的必考内容都没讲完,后面自然提分乏力。现在问题是基础都没补完,还叫同学去好好打基础,殊不知学校就是短斤少两,基础不全的源头。
(200赞再更新)
先讲些救急的措施,这部分内容,因为你们学校老师没讲或者没讲透,所以苦主无论如何都做不出第二问来:
1.集中精力去分析几何条件,讲题中几何复杂的条件转化为如几个方面:
①向量(垂直、平行)
②直线斜率(乘积,相除,相加减,甚至开方乘方,取对数)
将角度化成斜率是必然操作,然而用哪个三角函数?(不要死盯着一个tan,万一sin和cos给出的线段转化让计算更加简单,选错路线就是算到头大都算不出来的根源。)
③弦长和面积尽量摆在最后的选择,实在使用不了①②才考虑弦长与面积。
2.设未知量。
尽量选择中间点和中间线。计算的时候位于推理过程中间的线段和点,可以用最少的步骤得到其他线和点,从而最大化降低计算量。
立体几何大题也是这个原理,立体坐标的原点如果选得好,其他点的坐标会简单很多,算起来少很多计算项。
反正尽量往那堆圆锥大题蜘蛛网的最中间里面找,找到那个点和线,距离完美的标答也就不远了。
先将1,2这两个前置步骤练到最好,不要求一开始就练完整的圆锥大题,而是着重于练习这两个找条件与设未知量的步骤,这是第二问的基础。
这种找条件,选条件的过程,可以帮助你预想计算量,从而选择计算量最低的解法来做,这就是有些人可以十分钟做完圆锥,甚至更短时间的诀窍。
这里还有三个注意事项:
一。联立后的方程必须正确。很多人在带入展开的时候太过潦草,追求速度,于是就算错,凉在这一步是非常可怜的。务必先展开将y=km+h的平方每项都展开再去乘外面的系数a²,往往就是乘a²这一步算错。
二。最重要的二级结论
y=kx+h的时候
Δ=4a²b²(a²k²+b²-h²)这个只记括号里面的计算,可以快速用来算出k的范围,便于后面用不等式求定值。算Δ这步可以说,因为题目的系数变化会带来成千上万的计算,看到动不动就几万的系数,没算就先神经错乱了,这是前面4a²b²搞的鬼,知道这个结论可想而知有多重要。
三。反设直线:x=my+n
可以移项:y=x/m-n/m,照样套y=kx+h的运算,只不过k=1/m,h=-n/m,还是这样算Δ。当然一些经常喜欢自己推的同学,就容易记住:反射直线的时候Δ=(你TM自己代进去算下就记住了,不用刻意记)=4a²b²(m²b²+a²-h²)/m²
感觉只是括号里面主客颠倒,本来是a²k²在前,现在换成另外两个家伙乘在一起做主角了b²m²。同样后面的b²也替换成a²,但是减去的依旧是直线方程的截距平方(h²变成n²)
根本原因是1/m让x与y在坐标轴上呈现类似反函数的关系,造成对称运算。这可以辨别你自己是否算错了,如果算出来的式子会多出或少了什么,系数有些不一样(括号里面是有对称美的)。。。。。。所有这些都会在答案告诉你:丑就是错的。
完成上面那些,剩下的东西只是简单算一算(就像标答那样稍微算算就好了)。因为前置工作做得不好,所以你的解析几何第二问是算半天也算不完的:选择(线、点)比努力更重要。
上述内容,一些重点学校老师会在细节反反复复讲到烂。目前网课老师赵礼显等名师也是这么讲的,你听过之后,总结出上面的思路,在下次做题的时候,就容易做出来了。
现实中太多水老师,只讲个建系与设线,剩下就复读答案完事了。当然硬算也是能算的,只不过是翻十倍或者百倍甚至千倍的计算量,这种教学当然给你们添堵。
根本原因就是高考题设置就是让你先去想,将所有可能的解法都想下,从中找出最简单的解法来算。而不是一上来就算。计算这个谁不会?高考选拔的不是去工地扛水泥的民工。
下面讲些在你们眼里不正常,却非常好的解法。
1矩阵=行列式=线性代数)
椭圆,双曲线,抛物线,本质是在圆锥上的截面。什么意思?也就是说圆锥曲线是,三维的圆锥在二维(截面)上面的投影。(个别同学刷了那些四维空间在三维空间投影的短视频,我想你不应该白刷)。投影本身就是一种变换。很多同学喜欢学仿射变化,就是用圆来理解椭圆,可以将圆与椭圆的那些公式统一起来,理解起来更容易,不需要特别去记就能灵活运用。
线性代数的奥义就是变换(所有的变换)
圆锥是圆的仿射变换(某一种变换)
大家都是变换,就是一家人,你用我的,我用你的,很合理。于是这类解法在知乎上是有大佬贴出来的:
所以拿矩阵来解圆锥是很合理的。
好了,我废话特别多,你要顶住。
上世纪课改前,行列式可是必学内容,因为在处理变换的时候又非常巨大的作用。数列里面奇奇怪怪的递推式,本身就是一种变换,利用行列式求通项,这绝对比你学那些一大堆求通项方法要统一:死活凑不出来的配凑;记住不的不动点求解;意想不到的开根号、乘方,求对数;神出鬼没的添项,减去一个数、字母。
当然,行列式的运算量不会小。这不就中了某些人所言:圆锥大题考察计算能力!
确实,如果学了行列式,确实是大力出奇迹,,矩阵真的很能算。然而不教呢?上述论断就不成立了,高考题就变成了兵抓贼,谁先抓到最简单的运算解法,谁就能快速通关圆锥大题。所以,现在圆锥大题不考你运算,你别听那些老师瞎说了。
行列式高考可以用,已经问过很多人了,确实是不扣分的,不然你人教版无论AB版还是大纲版的教材都弄一本《矩阵与变换》选修是什么意思?

你没学过?我高中的时候也没学过。为什么?师资流失。很多学校有能力教线性代数的老师早就跑路了,能学懂这玩意,绝对脑子不简单了,岂会屈就那一个月几千的教师待遇。
线性代数不止能做数列题,还能做立体几何大题,还能做概率大题,还能做三角大题(说到这里你会不会心慌?).......还能把整张卷子秒了.......除非跳出数论大题吧(个别数论题也能解)。
一些同学想到这里已经蠢蠢欲动了:这哪是什么线什么性什么代什么数,分明是如来神掌,一招搞定整张卷子,练熟了快速通关数学,拿下150不是难事了。
且慢,少年。你的悟性如何?要用矩阵,可是要先辨别题中的变换是什么变换,这会影响你后面的连招,如果连前面找出题目对应的变换都做不到,你还是老老实实找些网课老师,练好上面救急措施。
天赋会决定你能否理解“变换------矩阵”这个过程,这是一个“蓄力------发功”的实际过程。当然努力去学线性代数,多找些B站视频看看,不懂看到懂为止也是勤能补拙的方式。如果勤能补拙失败了,说明你是真麻瓜了,别管巫师那些事了,让巫师跟巫师对线,麻瓜跟麻瓜玩吧。(练好你的救急措施)
想看数竞生五分钟做第二问的,等300赞。
我想你们还是等等吧,资料很多,元宵前后才能做完。
你们先看看导数大题怎么做吧。
https://www.zhihu.com/answer/1726685042
这里附加一下,极值点漂移的做法就是把两个(几个)根的方程进行消元,得到只剩下一个根的式子,带入题目不等式,转化这个不等式为函数(构造),最后还是操作一,再去求极值点。
说真的,这样做导数大题就有点像圆锥第二问,需要利用韦达定理消去根,而导数大题使用两(三)个根的方程,消去其中之一(之二)。
(2023年2月14日,祝大家情人劫快乐)
失踪这么久,大家有没有想我?想我是没用,因为我这些天被外星人抓走了,今天才刚回到地球。
人在山顶,刚下UFO,口袋里全是西北风。
上次我讲到哪里,我自己控制不住,我的键盘有自己的想法。
(其实我是去预习了《圆锥曲线论》),这本东西一打开我就恍然大悟了:
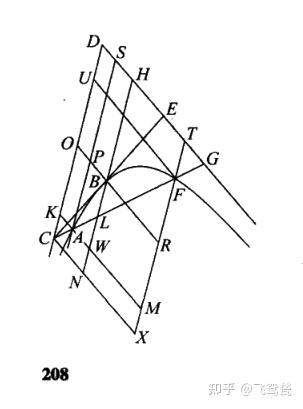
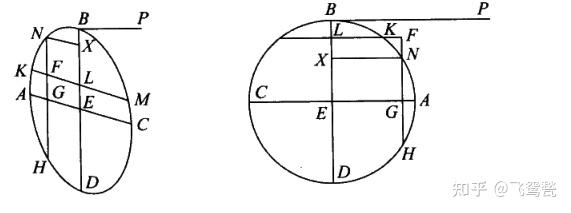

大师就是大师,古希腊大师果然令人敬佩,最复杂的题目往往用最简单的连招处理:
1疯狂加平行钱
2三角形相似(得到线段比例)
不是一家人,不进一家门,阿波罗尼奥斯,跟欧几里得是一伙的,《几何原本》里面也是疯狂加平行线,用相似三角形。
破案了,原来你看到的那些诡异的结论,画平行线跟相似三角形就出来,证起来就跟初中题一样。高一高二的同学可以试着学下。链接:《圆锥曲线论》
https://pan.baidu.com/s/1iBvvOKfX3LarW6k2UDoCug提取码:l7ps
链接《几何原本》:https://pan.baidu.com/s/1p0-r9CtHrRhjLQLxS9dnyw
提取码:bek1
想看竞赛生怎么做这第二问?
这了给学而思陈晨老师硬打一波广告,利益是相关的:他获得了报班数量,我获得了自由(我懒)。
作为一个十八县小城中学的学生,老师像复读机,数学题做不会,你怎么办?你还有陈晨老师。不需要学区房,不需要高昂的一对一,只要你能连网线,就能购买陈晨老师竞赛辅导课。把你学校没学的,教材删掉的统统加回来,技能库超级加倍,解题方法超级加倍,分数超超级加倍。
这里还给余正熙老师打广告:江西高考状元实力担当,价格又不高,绝对比其他老师的网课更全更细,想去就点他:
矩阵解圆锥大题,这里直接拷其大佬的链接吧:
听说线性代数可以在高中降维打击数列、圆锥曲线,具体是怎么应用的?其实,你们看看上面截的那几张图,如果化得开,都知道怎么去初中解法搞第二问了。

少学两本书,解析几何成了心腹大患。如图:

先用4-4的极坐标把题目条件转成三角形式,然后4-2跳过中间复杂运算,最后算个三角函数的辅助角,这样算极值,绝对比弦长公式,点到直线距离简单得多。
(不要私下问我那么多没用的东西,干就完事了。)
作为高中数学竞赛生,他们是怎样掌握高中数学中大量的技巧的? - 知乎 作为高中数学竞赛生,他们是怎样掌握高中数学中大量的技巧的?
你们高中数学所有的毛病,原因都只有一个: 教材不是B版
其他科目同类推荐,请付费咨询
有什么比网友自爆,更有说服力?
 新公网安备 65010402001845号
新公网安备 65010402001845号