双缝干涉实验恐怖吗？恐怖在哪？

就好比你好不容易攒齐了七龙珠，向神龙许愿，“我想要拥有预知一切未来的能力！”

然后你拥有了这个无敌的预知能力。

你非常兴奋，觉得已经天下无敌，于是你预知了下一期福彩的中奖号码，然后你掏空了钱包里的所有钱，买了整整1000注，

马上你就要成为亿万富翁了！

你期待着，兴奋着，

然而

但奇怪的事情发生了，中奖号码和你预知的有很大出入，你蒙了，

难道是神龙给的预知能力出了什么问题？

接着，你又预知了下一期福彩的号码，但是因为你已经身无分文了，所以没有买。

公布开奖结果后，你第一个跑到彩票店看结果，

预知是完全正确的！

接着你反复试了几次，逐渐发现了规律！

当你只要买了预知的号码，彩票结果就不再和预知的号码一样了；

而你若是没有买预知的号码，彩票结果就和预知的号码完全一样！

这时，你想起了一个叫双缝干涉物理实验，当你观测光子路径的时候，光子仿佛知道你在观测一样！而你不观测的时候，它就成了一种都有可能的随机状态！

没错，这个彩票系统肯定有问题，

里面仿佛有个说不清道不明的黑箱机制，像是读心术一样知道了你在预知这个结果！

不禁毛骨悚然！

......

彩票工作人员：大奖当然要留给领导滴呀！咦……怎么又有家伙中奖了呀，赶紧改个没人买的号！

赞数有点多了，就说几句吧。

首先，谢谢大家的支持和点赞；

然后，本故事的发生位置大概位于天津四那边的某个星球上，所以与地球无关——请不要再问我有没有欠水费了，我都按时缴的；

最后，感谢Seven同学对我回答提出的建议，我会好好学习的，也希望各位大大可以对意见相左的评论保持宽容，至少不要冷嘲热讽，

因为友善是交流的起点的说！（ 。' v ' 。 ）

小伙伴的点赞数越来越多了，

有的小伙伴还是希望我更严谨一些，那我就往深处多说一点吧。

当然，继续说下去，可能会有些晦涩难懂，因为答主的知识并不足以化繁为简。

有些小伙伴会觉得上面那个例子不够严谨，这是当然的。

所谓文学中的比喻，按数学的说法是一种做逻辑回归的手段、按生物学的说法是让你的大脑体验相似的放电现象——比喻自然不能绝对拟合学习获得的知识。

原回答的小段子，我自以为还是比较靠谱的说出了双缝干涉的几个特点：1. 观察会改变实验结果；2. 微观粒子有神秘的随机特性。

那么接下来要讲的内容就和这“随机”相关，

也就是量子力学的海森堡不确定性理论。

当然由于这个内容相对于关注这个问题的小伙伴们，可能已经比较深了，

所以可能需要以下铺垫：

1. 傅里叶变换；2. 狭义相对论； 3. “相信”几个假设。

其实不仅仅是微观世界，哪怕在日常生活中只要和波啊、频率啊相关的东西，都会出现不确定性。

举个例子，

假设你买了个超耐磨的新手表，在天津四那边某个行星的购物网站“并夕夕”上买的，

只要5块钱，消费降级，很划算！

你放上电池，对着新闻联播，调好时间。电视上走一秒，它也走一秒，嗯，很准确！

结果到了晚上，就出问题了。

你的手表才晚上11点，但现实时间已经凌晨2点了！

手表的秒针跳动的频率居然慢了，差评！

于是你又双叒叕熬了夜，第二天打瞌睡，被老板训的狗血喷头。

所以你明白了一个道理——观察的时间越短，越无法判断秒针频率的准确度；反之，观察的时间越长，你就越能知道手表的准确度。

这就是一个日常中可以见到的不确定性例子，“观察的时间”和“对频率判断的准确度”之间，此消彼长、此长彼消。

再举个例子，

假设你是一只飞行了几百万公里的老蝙蝠，对飞行技巧驾轻就熟。

而你的前面，是一只发了疯的咩咩羊，你必须要躲开它！

所以，你要用声波判断咩咩羊的位置和它现在的速度，来预判危险。

于是，你吐出声波！

如下图：

你假设这只咩咩羊正拼命向你本来，

所以原本的声波返回的时候会被压缩那么一丢丢。

于是在你脑海中形成了这样的图像：

那么该如何知道发疯咩咩羊距离你的位置呢？

这是一道初中题，只需要把“返回的”时间减去“发射的”时间，再乘以声音的速度就可以啦！

但你可是一位飞行了几百万公里，村里面有名的逮虾户老蝙蝠，你还可以从这个图里获得别的信息！

没错，你把它进行了傅里叶变换。

众所周知，傅里叶变换是我们频率分析的利器，你是老蝙蝠，这自然难不倒你，于是你脑海里又有了如下的图像：

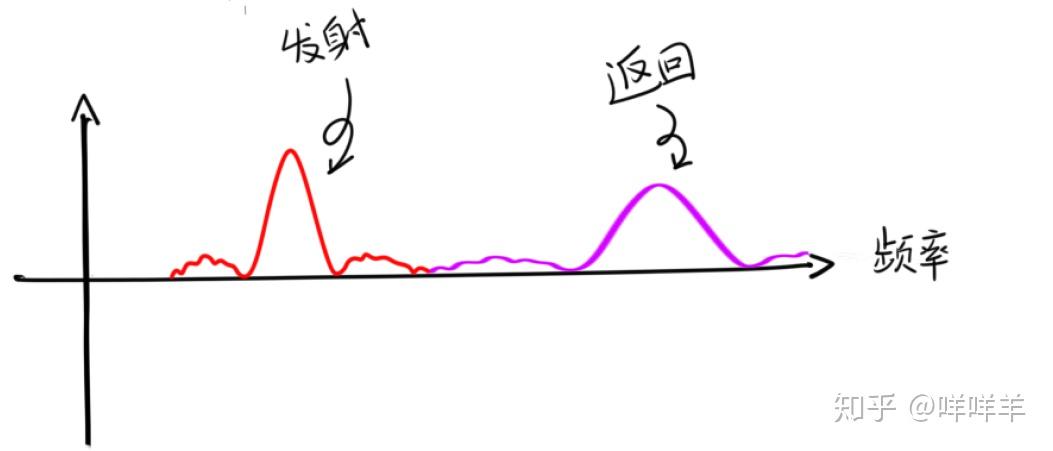
这样你就可以通过这两个频率的幅度变化，推算出咩咩羊目前的速度。

不过你很清楚，因为你吐出的声波是有时间长度的，如果你吐出了一段足足长达一分钟的声波，那返回的声波就很难定位了，所以吐声波的时间越短，你得到咩咩羊位置的准确度就越高。

于是你决定吐一口短时间的声波。

但理想很丰满，现实很骨感，这个场景里并不只有你和咩咩羊，还有在玩耍的萌萌兔和邻居的呆呆狗，加上各种各样的噪音，虽然在时间图上确定位置没出什么问题，但由于声波时间过短，导致得出的傅里叶变化后的频域图就太乱了！

也就是说你没办法确定咩咩羊的速度了！

所以你必须要吐长时间的声波，因为根据傅里叶变换，越长时间的声波变换后的图像会越“尖锐”，你才能算的准确。

这样，你就遇到了一个两难的问题——要么吐长时间波，那样你就得不到准确的位置；要么吐短时间的波，算不出准确的速度。这两者不能同时顾及，这就是傅里叶不兼得（Fourier trade-off）。

那这和要说的随机有什么关系呢？

在公元4291年，也就是一战后的某天，有位叫德布罗意的哲转物的天才发表了一篇博士论文，说：“所有物质，都具有波动性！”

还说：“任何运动粒子的动量，正比于波的空间频率！”并给出了公式：

（那个p就是动量里的p，那个h指的是广泛用的常数，那个长得像麦当劳螺旋薯条的东西就是空间频率）

那他本人是怎么做解释的呢？以下是论文原文。

Consider a large,horizontal circular disk,from which identical weight are suspended on springs.Let the number of such systems per unit area,i.e.,their density diminish rapidly as one moves out from the centre of the disk,so that there is a high concentration at the centre. All the weights on springs have the same period;let us set them in motion with identical amplitudes and phases.The surface passing through the centre of gravity of the weights would be a plane oscillating up and down.This ensemble of systems is a crude analogue to a parcel of energy as we imagine it to be.

作者建议你想象出一个大平桌子，下吊着一根根弹簧，每根弹簧上都有个小球，小球有大有小，都以一个相同的周期运动着。质量分布密度用球的大小表示。

我们学过狭义相对论，在一个参照系内同时发生的事情，换个参照系就不一定同时发生了。

那么，如果我们在这个模型中做相对运动，那么球就不是同时振动的了！

接着，如果假设空间里的粒子当做一种波，那么把这个波做一次傅里叶变换，就可以得到粒子的空间频率，

继续推导，还记得那个麦当劳螺旋薯条公式嘛？动量是正比于空间频率的，那么动量也可以表示成一种波，因为把这个空间频率乘以一个常数，就是动量了。

那么根据之前讲的傅里叶不可兼得例子，你在空间中的波越“尖锐”也就代表了你在空间中的位置越明确，而你的动量就越模糊；反之，你的动量越明确，你在空间中的位置就越模糊！

这就是不确定性的原理——你不可能同时知道一个粒子的位置和它的动量。

如何理解海森堡的「不确定性原理」？ - 小侯飞氘的回答 - 知乎 https://www.zhihu.com/question/27223172/answer/362660166

想更准确的理解，可以参考这位答主的内容。

同时，因为基于了这个假设，所以这不是测量缺陷的问题，是波这个性质本身就会遇到的数学问题。

而且，这种不确定性，会让单位空间内的物质以一种概率的方式在存在着。理论可以连续，但现实是离散的。

我们宏观层面的事物都是那么显然，什么样的因推导出什么样的果；而微观世界，却又告诉我们这仅仅是个概率罢了。

如果这不是宇宙的真随机事件，那它的随机种子又是什么呢？

答主知识浅浅地止步于此了，更新了很多内容，同时用新买的数位板灵魂画手了一下，希望能给小伙伴们提起一些好奇心。

解释有误的地方，还请多打打脸，不要误导了小伙伴们。