有没有什么东西画完三视图还没办法确定的?

这么多天了，居然还没有一个答案直截了当地给出一个例子……

那我来举个例子好了。一个物体，三视图都是下面这种「四饼」的形状。它是个什么呢？

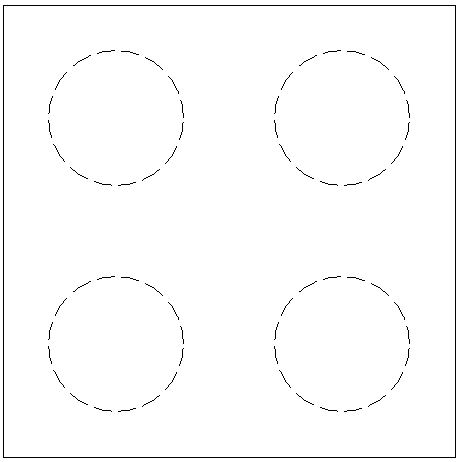
很容易想到，它可以是一个正方体里面挖掉 8 个球形的洞：

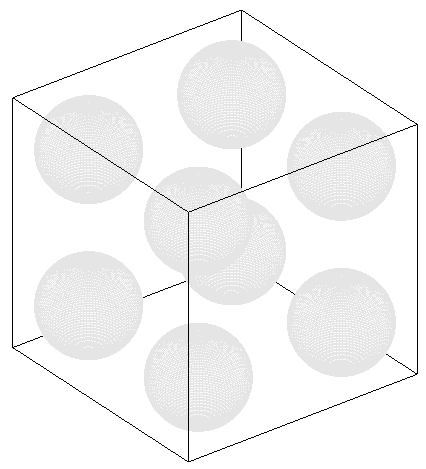
但事实上，这 8 个洞并不需要全都挖掉。

比如，只挖 7 个洞，得到的三视图仍然是三个「四饼」。这样的物体有 8 种。

也可以只挖 6 个洞，能满足三视图均为「四饼」的物体有 16 种。

还可以只挖 5 个洞，能满足三视图均为「四饼」的物体有 8 种。

最少可以只挖 4 个洞，只要这 4 个洞互不相邻即可。这样的物体有 2 种，如下图。

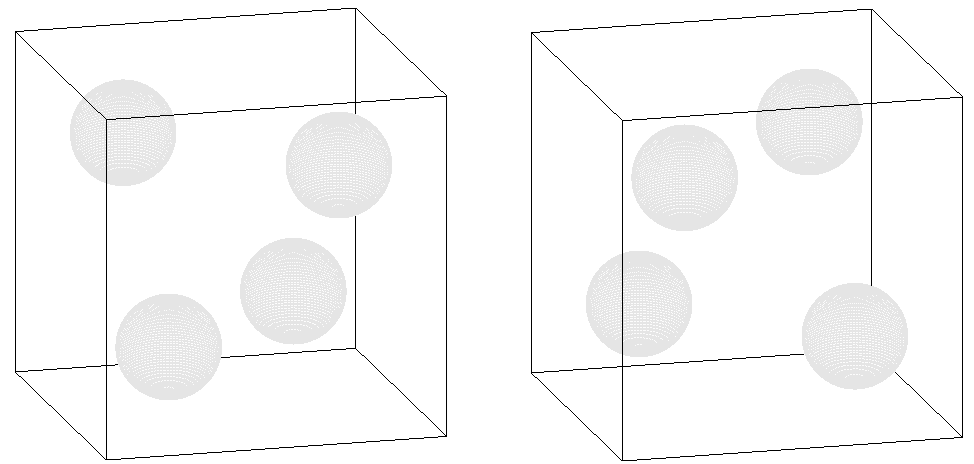
也就是说，已知三视图均为「四饼」，物体的形状仍不能确定，且有 1 + 8 + 16 + 8 + 2 = 35 种可能。

评论区里不少知友指出，我说的「不同物体」经过旋转之后可以重合。

我之所以在答案中没有把这样的物体合并，是因为一般情况下，三视图包含了物体的朝向信息。

如果要合并的话，那么挖 8、7、5、4 个洞的物体其实分别只有 1 种，挖 6 个洞的物体有 2 种（两个洞可以位于面对角线上，也可以位于体对角线上），合计 6 种。

不出所料地，评论区有不少人挑刺说这是个空心物体，让我找一个实心的例子。

@刘子璇 比较早地提出了一种思路：一棵树上结 8 个果。不过这几天我一直没想好该怎么处理果子和树枝之间的遮挡关系 —— 如果果子挡住了树枝，说明果子在靠近观察者这一侧；如果树枝挡住了果子，说明果子在远离观察者这一侧：这样，通过虚线就能分辨果子的位置了。

今天我突然来了灵感：把树枝放在无论如何也不会被果子挡住的位置就好了！于是我就造出了下面这个例子。我把果子由球形换成了立方体形，这是为了避免树枝与果子相贯处出幺蛾子。

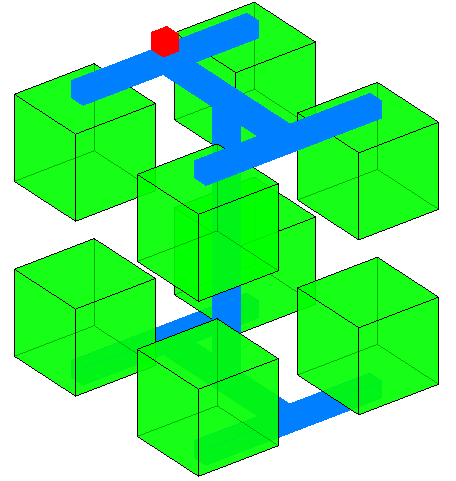
这个东西的三视图如下。在主视图和左视图上，果子与树干、树枝完全不会互相遮挡；在俯视图上，上层的树枝会挡住果子，而不是果子挡住树枝。

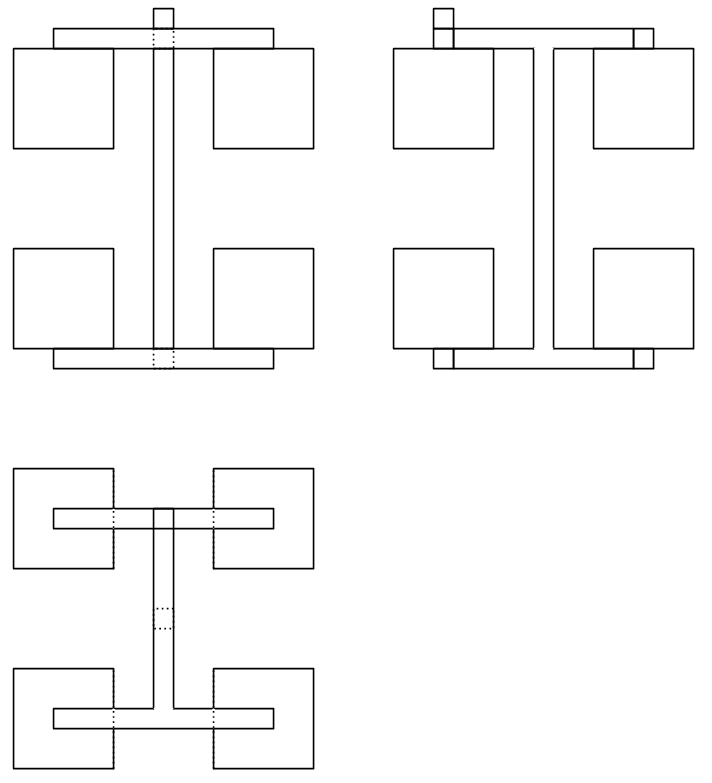
好了，现在可以摘掉一部分果子了。只要摘掉的果子互不相邻，三视图都不会发生任何变化。这跟在我的原始例子中不挖一部分洞是等价的。也就是说：

• 结了 8 个果子的树，有 1 种；
• 结了 7 个果子的树，有 8 种；
• 结了 6 个果子的树，有 16 种；
• 结了 5 个果子的树，有 8 种；
• 结了 4 个果子的树，有 2 种。

合计 35 种。

什么？你问我那个红色的「小啾啾」是干什么用的？它是用来打破对称性的，省得你们说有些树经过旋转之后可以重合。

评论区里 @Yehowah 提供了另一种灵感，我来把它画出来。他提出的物体是一个「烤串」：

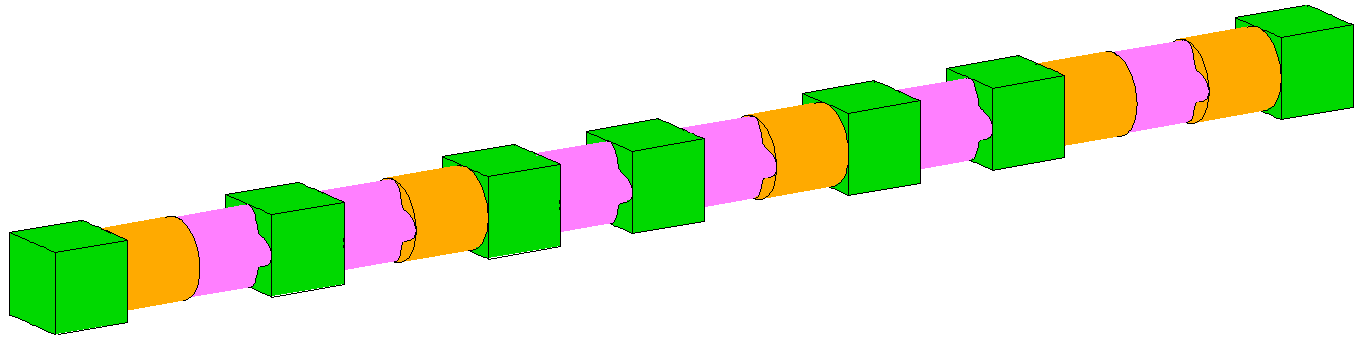
「烤串」中的每一截，主视图和俯视图都是一个正方形，而左视图有三种：正方形、圆形、四瓣花。整个「烤串」的三视图是这样的：

只要烤串的相邻两截互不相同，整个烤串的主视图和俯视图就会是一串正方形相连，没有什么信息量。而整个烤串的左视图，则是烤串上每一截的左视图叠加；既然最左边一截是立方体，那么左视图上的圆形和四瓣花就都是虚线。在这种情况下，我们完全无法推断从第二截往后每一截的具体形状。若整个烤串有 截，则后面各截的形状有 种可能：每一截不能与前一截相同，有 2 种选择；还需要刨除整个烤串「完全不含圆柱」和「完全不含四瓣花」的两种可能。