如何以“废后喝下毒酒前，含泪问我‘你会解偏微分方程组吗？’”为开头写一个故事？

废后喝下毒酒前，含泪问我：

“你会解偏微分方程组吗？”

我递上鸩酒，恭恭敬敬：

“母后放心，我不仅会偏微分，还会全微分、多元函数复合求导……”

我抬起头看着伊，心坎里便禁不住突突地发跳，赶紧弱弱地补上一句：

“积分也会。”

结果伊只是无力地点点头，又问：

“你懂经典力学吗？”

我心中一动，便壮着胆子朗声作答：

“当然，我不仅懂经典力学，我还懂相对论和量子力学……”

伊长叹一口气，缓缓道来：

“自从被打入冷宫的那一天，我就料到今天的结局。好在你已经长大，我也了然无憾。只有一事，我一直想不通。如果得不到答案就去死，那我死也不能瞑目。“

“当年我在这冷宫之内，闲来无事，便手搓一个经典力学模型，做做思想实验解乏。可日思夜想，竟越发难解……”

伊从头上拔出玉簪，如雪般长发散落一地。只见伊刺破手指，用血在三尺白绫上写下——

一张图：

我倒抽一口冷气，扑通跪下：

“孩儿请母后明示。”

伊微微一笑，一如多年以前，倾国又倾城。

“经典牛顿力学模型罢了。”

我不敢多言，只得垂首听下去。

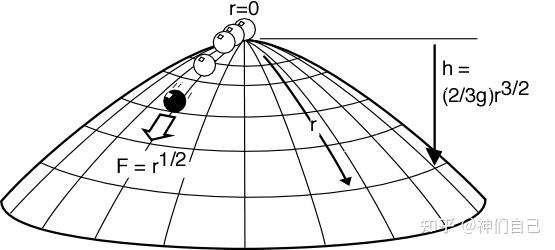
“众所周知，如果把一个小球放在拱顶的顶点上，它无法保持稳定状态，必然会滚下去。但是在理想模型中，排除一切微扰，小球可以永远停留在顶点上。”

“不过，我设计了一个特殊的拱顶。如果把球到顶点的曲面距离称为r，球到顶点的垂直距离称为h，那么曲面可以用以下方程描述：”

血不够用了，伊又刺破一根手指。

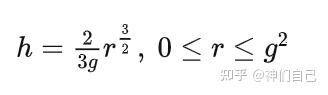
“曲面是绝对光滑的，所以小球只受到重力。重力沿曲面切线分量是：”

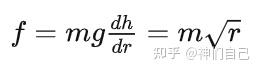
“根据牛顿第二定律，距离r对时间t的二阶导数就是加速度，易得：”

说到这里，废后又叹了一口气：

“孩儿，抬起头来。”

我抬起头。

“孩儿，你既然会解偏微分方程，不如现场解一下，即可得到小球在曲面上的动力学方程。记得边界条件是，t=0时刻，小球在顶点r=0的位置。”

我大惊：

“母后恕罪！孩儿虽学过偏微分方程，可时日已久，再加上近日沉迷宫斗无法自拔，所以……不如请母后指教……”

伊忽地站起，两手搭在髀间，张着两脚，正像一个画图仪器里细脚伶仃的圆规。

我愕然了。

果不其然，母后的巴掌准确地呼在了我的脸上。

“哈！不学无术的东西！如此不成器，宫斗怕也难活过第一集吧！看来还真是你爹亲生的，和你父王一个样！”

伊含着泪，重重地坐下。

“也罢，不如今日就告诉你真相。”

“这个偏微分方程有2个解。显然，r=0是平凡解，也就是小球永远在顶点静止。然而第二个解是：”

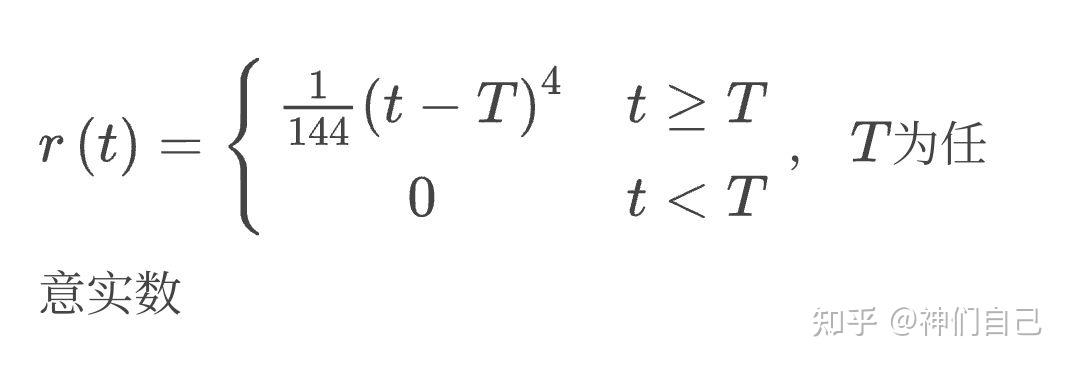
“这个解在物理上直观的解释是：小球先在拱顶位置停留任意时间T，然后滚下来。”

“那么问题来了：根据牛顿第一定律，物体受力了才会改变运动轨迹，不受力就永远会改变运动轨迹。这个球先是停在拱顶一段时间T，然后改变轨迹滚下来，请问是谁改变了小球的运动轨迹？”

我的后背开始发凉。

“按这个解，小球可以在顶点停留任意长时间，它想什么时候下来就什么时候下来。那岂不是意味着，牛顿力学是非决定论的？”

“母后，莫非您的意思是，这是一个……悖论？”

“我在此冷宫面壁十年，也未能参透，所以，看来是的。”

“那您这杯毒酒还打不打算喝了？酒都凉了。”

伊大哭：

“孩儿啊，如果连经典力学理想模型都不会解，我有何面目见先帝牛顿于九泉之下？！”

我也大哭：

“母后啊，我苦读十余载，只为早日成为皇家认证做题家，将来完成大统一理论的大业。没想到今日连一个小破球都搞不定，果然一切都是幻觉，物理学tm的不存在！”

我端起杯子：

“母后，我先干为敬。”

The End

这个悖论，就是著名的“诺顿穹顶”。

如果你真想了解是怎么回事，可以看看我的这篇回答：

不过我得先警告你：20年来，无人能解。

壮士，干了这杯酒，你行你上。

我正在写一个太空/航天主题的长篇科普作品，我把它叫做《太空三部曲》系列，这是我有生以来写过的体量最大、内容最多的科普，包括物理、天文、航天、生物各领域，信息量很大，我想挑战一下……

三部曲第一部《逃离地球表面》，正在知乎专栏首发连载，欢迎大家踊跃试吃~

点这里可以看：

逃离地球表面：从地球大炮到火星探索

(99+ 封私信) 牛顿真有传说的那么厉害吗？ - 知乎 (zhihu.com)

飞机的升力仅仅只是由于伯努利原理产生的吗？ - 知乎 (zhihu.com)

为什么大刘说太阳氦闪时必须离开太阳系？ - 知乎 (zhihu.com)