iir和fir滤波器的区别？

上次，咱在《干货周记：对FIR的本质理解（番外篇8）》中，简单理解了FIR，这次，咱接着填坑，再聊聊IIR。

与天生自带“数字光环”和“DSP基因”的FIR不同，IIR更多是基于物理世界的，Roy则会更简单粗暴地，把它看作“模拟滤波器”的数字版复刻。

一句话定义

IIR全名是：Infinite Impulse Response，即“无限长单位冲激响应滤波器”，和FIR类似，它也是一种常用的数字滤波器。不同的是，其脉冲响应是无限长的。

老规矩，不管它牛鬼蛇神，咱先用”照妖镜“看看它的数学本质：

和FIR类似，IIR本质上也是一堆系数，但它是两种系数，分别对应历史输入和历史输出，所以本质上，设计IIR，就是追求相应系数的过程。

发现了么，与仅与输入相关的FIR相比，IIR多引了个反馈支路，也正是这一点，使得其脉冲响应是无限的，造就了另一个有趣的灵魂，这个具体咱后面会聊到。

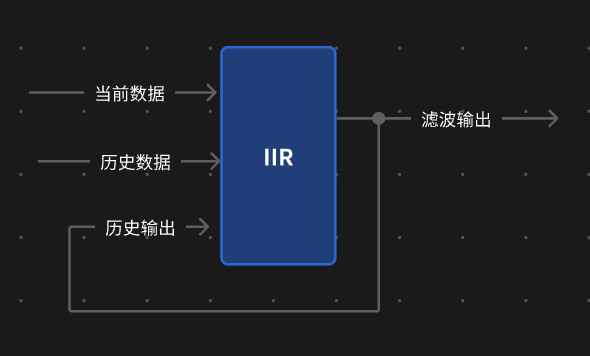
话说回来，IIR在时域长这样：y[n]=b0*x[n]+b1*x[n-1]+b2*x[n-2]+...a1*y[n-1]+a2*y[n-2]+...给“差分方程”穿上正装，其更严谨的模样：

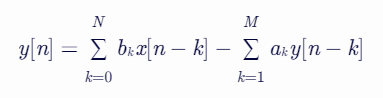
其中，y[n]是输出，x[n]是输入，b_k为前馈系数，a_k为反馈系数（a0通常为1），M是反馈系数数量，N是前馈系数数量（不包含a0）再看看IIR的频域，长这样：

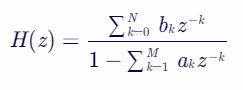
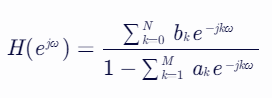
架构上，大致长这样（以直接Ⅰ型，2个二级级联为例）：

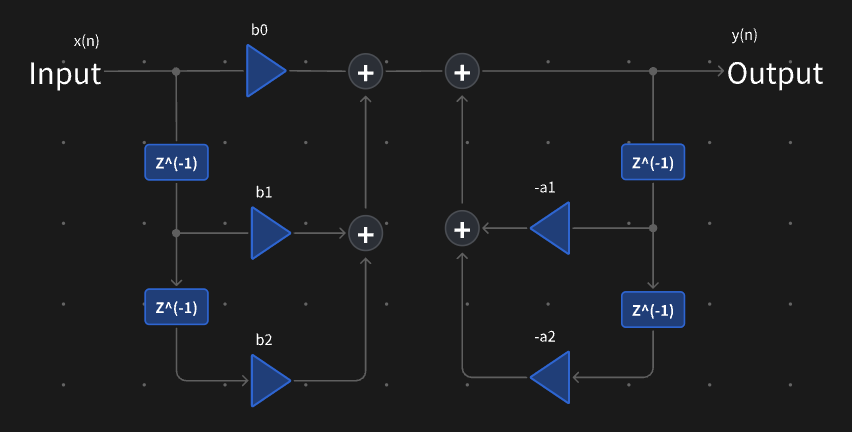
最直观的感受，即IIR的数学表达，似乎没有FIR那么简洁。而且它还竟然还分母式，这意味着，IIR不仅有零点，也会有极点，既然有极点，那它也可以是个”潜在风险“携带者。当然，这与其”递归“基因有关，咱下面来简单看看，IIR究竟是怎样一个存在。

IIR，一个不同的灵魂

如果说FIR擅长法术袭击，那么IIR就纯靠物理攻击。上期咱们聊FIR时，大谈特谈卷积等信号处理的思路，得转变一下了，因为，IIR完全不是这一卦的。

一、怎么理解IIR的“无限长”

从它的差分方程中可以看到，IIR的输出不仅和当前与输入值有关，而且还和过去的输出值有关。也就是说，IIR是递归结构，使得它任意时刻的输出，身上都有所有历史输出的影子。

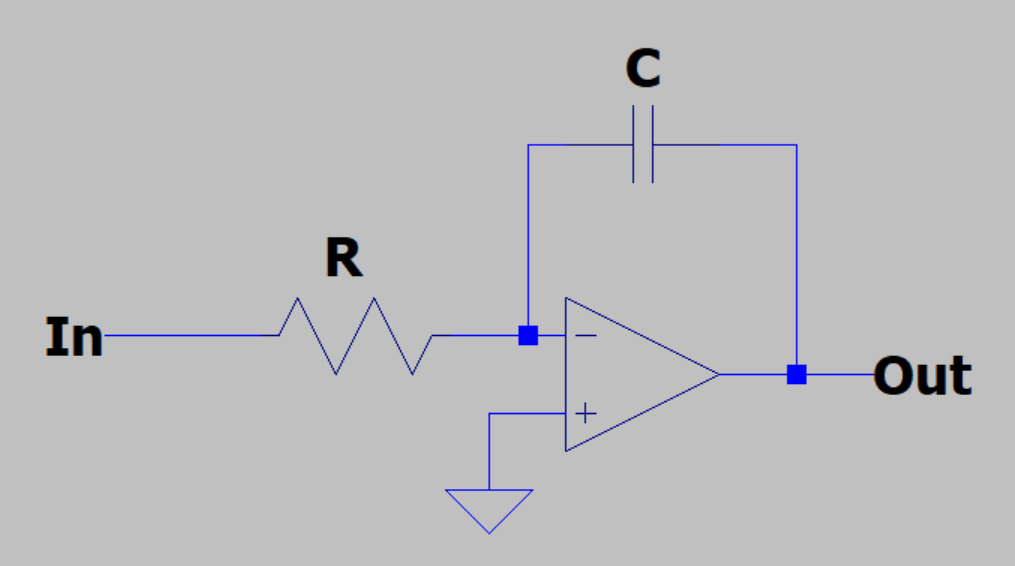
再直白些：IIR任一时刻的输出，对其之后所有的输出值都有影响。而且理论上，这种影响，将会无限递归地传下去。刚咱也提到过，IIR也可视为模拟滤波器的数字映射，它们在很多特性上也是相似的，在一阶积分滤波器上，也有类似“无限”的概念，比如积分器的“记忆效应”，它经历了一次脉冲响应后，Vout电压在理论上，是无限趋近于零，但不完全等于零的（仅供理解用）。

二、IIR有什么特点？

这部分，参考资料，遍地都是，咱就简单突出三个点吧：

频率选择性：强。由于IIR传函的极点可出没于单位圆任何位置，所以，它可用较低阶数，实现更高效的频率选择性。同样的目标频响，IIR所需要的系数和阶数，远小于FIR（通常相差10倍级），效率很高，也很适用于很多小芯片场合。

相位可控性：弱。毕竟脱胎于模拟滤波器，再加上反馈递归结构，IIR滤波器的相位非线性，且很难设计与预测，针对相位敏感的场合，要么直接上FIR，要么需给IIR加单独的全通调相网络，做相位矫正。当然设计时，也可在“矮子里面拔将军”，基于相位特性好的模拟滤波器（如贝塞尔滤波器），做IIR映射。

稳定性：弱。递归结构的IIR，有自激震荡的风险。这主要来自两点：一是IIR的极点位置太自由，设计时需要放在单位圆内，且留有裕量。二是，由于数字计算的精度有限，运算中会有舍入处理，这有可能会产生累积误差甚至寄生振荡。

三、实战启发示例1：

咱还拿上面这个，一阶积分滤波器，举个实际。不难理解，其s域传函为：H(s) = Vout/Vin = (1/sC)/(R+1/sC) = 1/(1+sRC)

基于此，我们可把上述s域传函，映射到数字z域中去。不同方法对应的幅频和相频特性，也有所不同，咱下面以“一阶后向差分法”为例：令s = [1-z^(-1)]/T（映射公式），有：

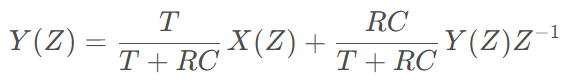
显然，其对应的差分方程为：

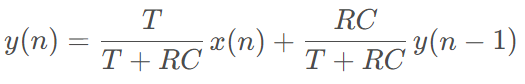
如此，咱就神奇地把“一阶RC积分滤波器”，映射到了“IIR数字滤波器”。（对应系数：a0=T/(T+RC)),b1=RC/(T+RC)）。

示例2：某款电容传感器的手册中，有提到过基线跟随寄存器，工程师可基于硬件应用环境，来手动调整基线Baseline的跟随速度，如下：

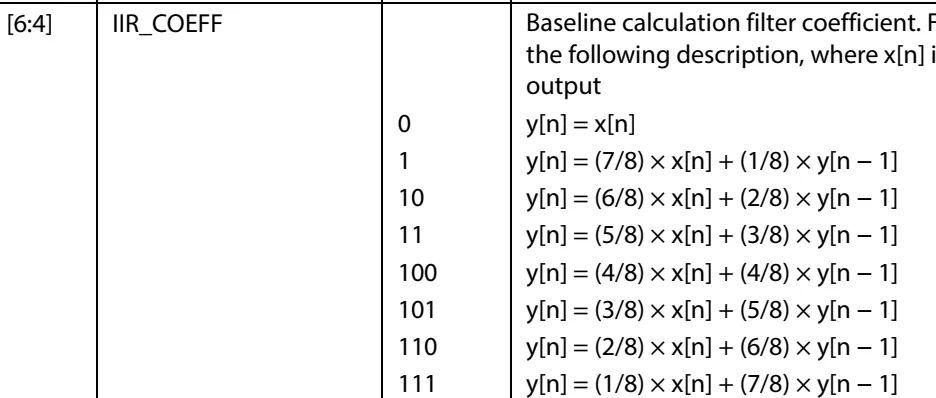
有了之前的经验，咱明显可以看出，这明显是个基于“一阶后向差分法”得到的一阶IIR，通过简单设置，即可实现不同速度的基线跟随。这里为啥用IIR呢，因为在小传感器中，IIR的实现效率高，且这种应用对相位不敏感。

不过，这里Roy其实也有个疑问：直观理解下，从000到111，应该是越往下对高频抑制的越狠（000时不作为，输出完全等于输入，111时大多数权重依赖于上一个输入，应该比较能“去抖”，对高频压制力较大）

但从数学上分析，越往下，极点其实是越远离0度的，这意味着越往下对高频压制的其实越松，刚好和上面的直观理解是相反的。

如有大神路过，还请帮忙解答下。

示例3：

前面说过，IIR的反馈结构，导致了它不太好直接设计，通常都是基于模拟滤波器，映射到数字域，得到其对应的“数字孪生IIR”。再加上稳定性的约束，咱很难正向设计超过三阶的IIR。

基于此，双二阶滤波器（Biquad filter）就很吃香了，因为它既能提供足够的滤波效果，又不至于因阶数过高而导致系数敏感性增强。还能够级联实现多级应用。关键是它的实现结构也很灵活，甚至可根据不同的计算平台，去做针对性的选择。

再加上其执行效率高，低阶低延迟，很适合用在对功耗和延迟都敏感的场合，比如下面的ANC滤波器，下面的FF filter和FB filter大都是基于IIR搭起来的。

具体要怎么设计IIR？

IIR的具体设计，可以手算，也可以靠工具。手算的话，除前面提到的一阶前差分、一阶后差分法外，更会用更灵活下述方法。

一、双线性变换法。这一招，是基于“传递函数”的影子映射。其核心奥义：直接把传递函数，从模拟域“共形映射”到数字域。通俗地讲，它把模拟滤波器，通过“公式通道”，直接“通灵”到了数字z域。

为啥叫双线性呢，Roy觉得，这主要体现在，从“s域”到“z域”的映射公式，其分子和分母（即输入和输出）都是线性运算。

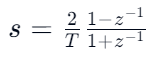
二、脉冲响应不变法。这一招，是基于“时域脉冲响应”的影子映射。其核心奥义：在数字域“模仿”模拟域的脉冲响应，再反过来得到，其对应的z域表达。可想而知，它的时域逼近效果很不错，但也可能会有些频域副作用（如混叠）。

三、工具/程序设计法：

生命苦短，时间宝贵。咱还是建议基于工具来设计，除了上期提到的Matlab的fdatool之外，也可以用代码做轻量级设计，简要方法，大致如下（仅供参考）。基于Matlab工具设计：

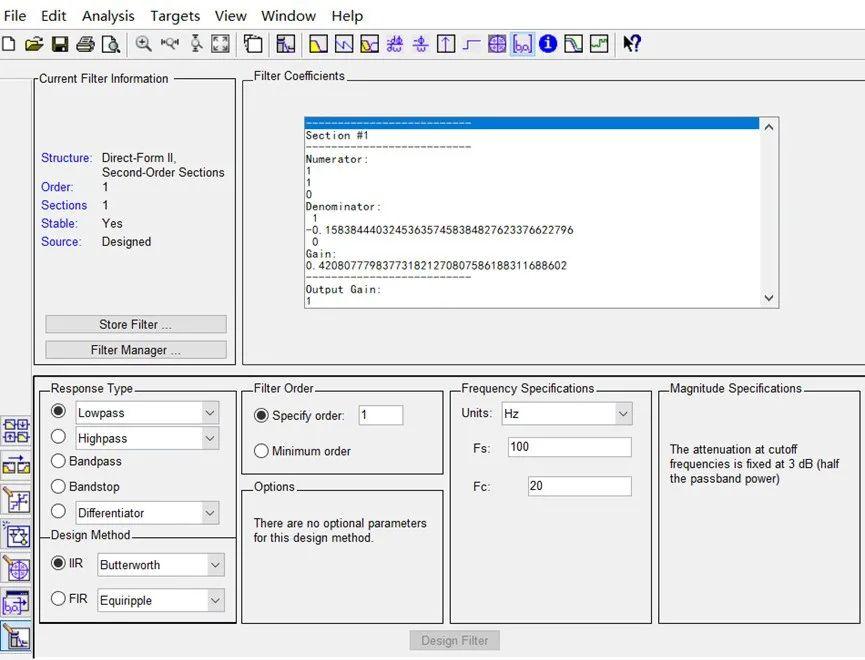
基于程序语言设计（Python, Matlab等均可）

一眨眼，又快码了3000字了，字数限制，只能先写到这了，下面几篇文章建议可一起参考：干货周记：对FIR的本质理解（番外篇8）

干货周记：轻松搞懂“运放稳定性”和“零极点操纵术”（番外篇4）

干货周记：三分钟弄懂零极点图（下）（番外篇3）

干货周记：三分钟弄懂零极点图（上）（番外篇2）

FIR也好，IIR也罢，还都是数字滤波器范畴，我们下次再找机会聊聊，身处另一个世界的：模拟滤波器。

End

Roy个人观点，仅供参考。

如果你对数码产品、英语学习和励志成长也感兴趣，也可关注各平台上的同名视频账号：微博、抖音、视频号，B站、小红书：科技朋克Roy，知乎：Roy